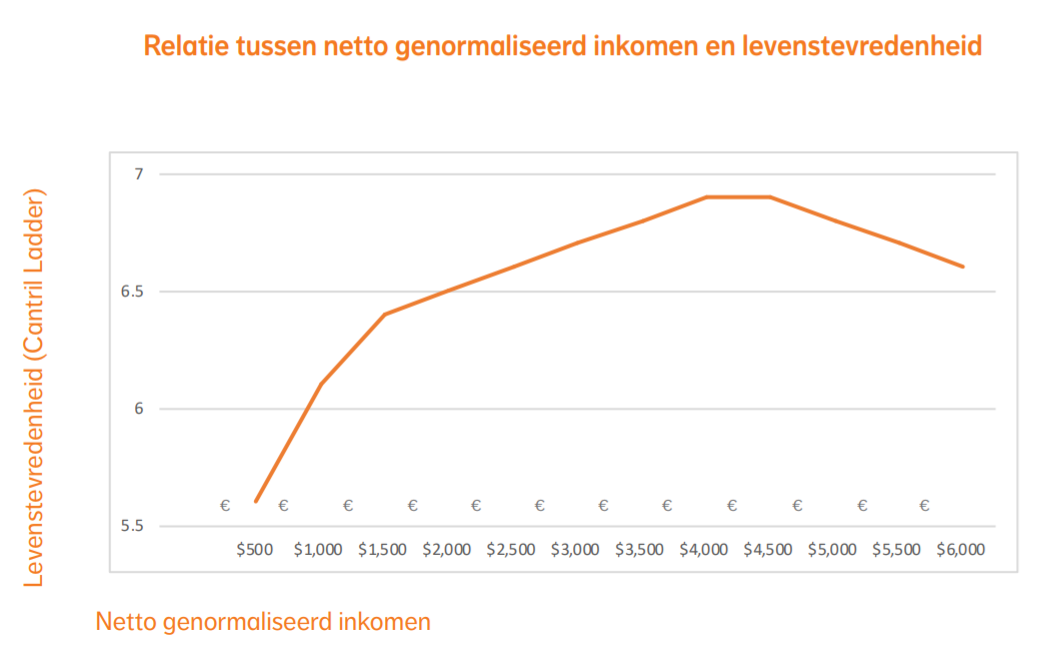
Geluk daalt bij de hoogste inkomens? Ongefundeerde stelling

Posted on December 16, 2018 by Andreas Tirez

Een paar weken geleden publiceerden de UGent en levensverzekeraar NN een nieuw luik van hun Nationaal Geluksonderzoek. De blikvanger was deze keer dat meer geld wel degelijk gelukkiger maakt, maar slechts tot een bepaald niveau. Vanaf een maandinkomen van 4000 euro wordt de Belg gemiddeld niet gelukkiger meer. Meer nog, vanaf 5000 euro en meer zou de Belg gemiddeld ongelukkiger worden. De onderstaande grafiek komt uit het persdossier van het onderzoeksteam.

Het is wellicht onnodig te zeggen dat de afname van geluk voor de hoge inkomens veruit de meeste media-aandacht trok. Voor professor Annemans (UGent), betrokken bij het onderzoek, bewijzen de cijfers dat we het economisch systeem moeten herdenken om het geluksniveau op te krikken.

Dat er een verzadingspunt en zelfs een terugval is, vind je ook terug in ander, internationaal onderzoek. Een artikel van uit Nature Human Behaviour (‘Happiness, income satiation and turning points’) van begin dit jaar kwam tot eenzelfde resultaat. In het artikel stellen de auteurs dat er een verzadigingspunt optreedt op 95.000 dollar per jaar wat betreft levenstevredenheid. Wat betreft emotioneel welzijn ligt het verzadigingspunt tussen 60.000 en 75.000 dollar. Nochtans, zo stellen de auteurs, zijn er andere onderzoeken die geen verzadiging of terugval vaststellen. De wetenschap is er dus nog niet uit.

In het artikel uit Nature Human Behaviour worden er een aantal redenen opgesomd waarom vorige studies die concludeerden dat er een verzadigingspunt is belangrijke beperkingen hadden. Zo gebruikte een belangrijke studie categorische variabelen voor de inkomens. Een andere beperking is de bron van data: gegevens uit bevragingen zijn minder betrouwbaar dan uit een fiscale inkomensdatabank.

Gebrek aan data

Ten slotte is er het gebrek aan data, waardoor sommige studies geen uitspraak kunnen doen over het feit of er een verzadiginspunt is in de relatie tussen inkomen en geluk. Dat komt omdat het verzadigingspunt erg hoog ligt. Dat geldt ook voor de Belgische studie. De geciteerde inkomens uit die studie zijn immers netto-inkomens en zijn genormaliseerd, wat wil zeggen dat ze rekening houden met het aantal volwassenen en kinderen per gezin. Een genormaliseerd netto maandinkomen van 4500 euro komt dan overeen met een netto inkomen van 9450 euro voor een koppel met twee kinderen. Met een dergelijk hoog inkomen zit je makkelijk in de top 1%.

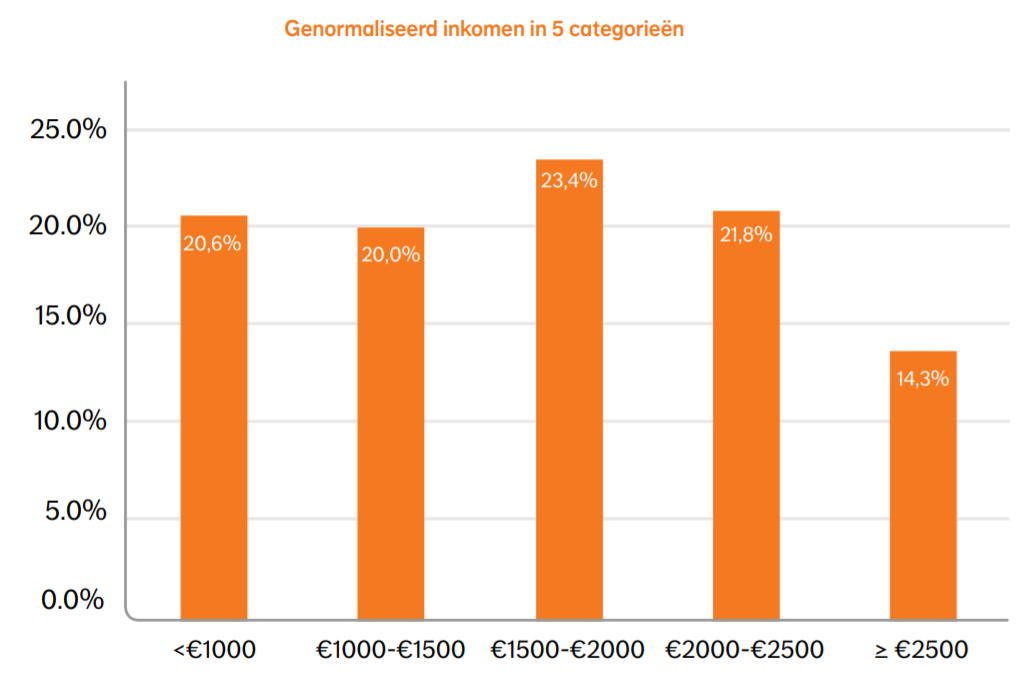
En die top 1% participeert niet makkelijk in allerhande onderzoeken die ook peilen naar het inkomen. In het persdossier zat de onderstaande grafiek met daarin het percentage van de 3770 respondenten per inkomenscategorie: uit deze grafiek blijkt dat het aantal respondenten al afneemt voor inkomens vanaf 2500 euro.

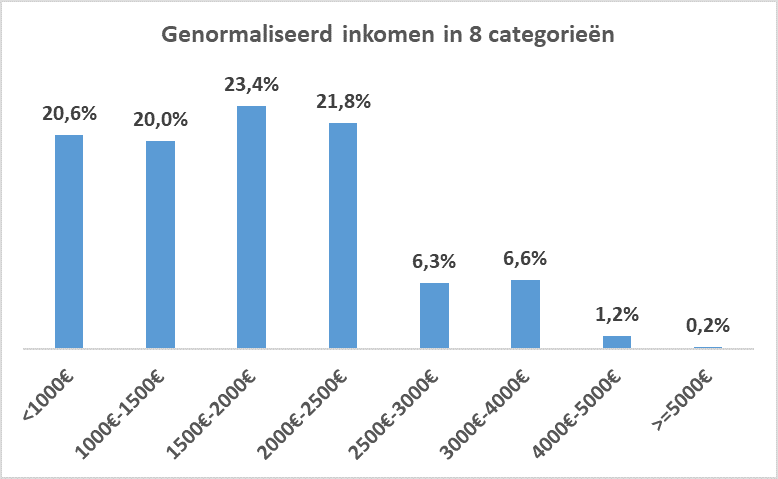
Het is opmerkelijk dat deze slechts gegevens geeft tot 2.500 euro, terwijl de blikvanger van het onderzoek gaat over wat er gebeurt vanaf 5.000 euro; dat is precies het dubbele. Ik heb de data dan opgevraagd bij de persverantwoordelijke van het onderzoeksteam en zij gaf me de onderstaande grafiek mee.

Uit deze grafiek blijkt dat ook in dit onderzoek het niet goed gelukt is om voldoende respondenten te vinden in de inkomenscategorie waar het om draait, wanneer men een goed gefundeerde uitspraak wil over het al dan niet bestaan van een verzadigingspunt. Van de 3770 Belgen die aan het onderzoek deelnamen, had slechts 0.2% een genormaliseerd inkomen van 5000 euro of meer. Het gaat dus over 6 tot 9 personen op 3770. De opmerkelijke conclusie van het onderzoek dat een netto-inkomen van 5000 euro of meer ongelukkiger maakt lijkt dan ook op los zand gebouwd.

Bijkomende informatie over het onderzoek

Het bovenstaande had ik ook in een opiniestuk geschreven op vraag van De Morgen. De dag erna was er een reactie van professor Annemans die onder meer inging op het zeer beperkt aantal respondenten. Hij schreef het volgende: “Bij zo’n analyse dragen álle deelnemers bij aan het eindresultaat. Stel u voor dat de bevinding, met name dat de levenstevredenheid opnieuw licht daalt bij de hoogste inkomens, gebaseerd zou zijn op slechts een handvol waarnemingen, zoals Andreas suggereert. Onze analyses steunen op honderden, zelfs duizenden waarnemingen. Het gevonden verband was bovendien statistisch uiterst significant.”

Gezien deze uitspraken me nog nieuwsgieriger maakten naar de gebruikte methode nam ik contact op met professor Annemans met een aantal vragen. Uit zijn antwoord bleek dat de gegevens verzameld zijn door middel van een bevraging, waarbij de respondenten moesten aangeven in welke inkomenscategorie hun gezin zich bevindt (met intervallen van 500 euro). Deze inkomens werden vervolgens genormaliseerd volgens gezinssamenstelling.

De professor schreef ook dat de eigenlijke analyse gebaseerd is op een multivariate regressie, corrigerend voor o.a. leeftijd, geslacht, opleidingsniveau,… waarbij zoals in ander onderzoek de inkomensvariabele ook wordt gekwadrateerd om na te gaan of er inderdaad een kwadratische relatie is. De kwadratische term in de analyse was zeer significant (p-waarde 0.00003), aldus de professor.

Dat riep bij mij weer een aantal bijkomende vragen op. De professor verwijst naar een kwadratische term in de multivariate regressie. Dat betekent echter niet meer dan dat er getest wordt of het inkomen een andere dan een constante, proportionele relatie met levenstevredenheid heeft (in jargon: is de relatie lineair of niet). Uit ander onderzoek weten we immers dat de levenstevredenheid inderdaad stijgt met het inkomen, maar dat die stijging niet in dezelfde mate blijft toenemen, naarmate men een hoger inkomen heeft. Er is dus geen constant stijgende levenstevredenheid naarmate het inkomen toeneemt (het verband is niet lineair).

Om een rekenvoorbeeld te geven: stel dat we vaststellen dat als het inkomen van 2000 naar 2500 euro stijgt, de levenstevredenheid gemiddeld gezien stijgt van 6 naar 6.5. Dat betekent dat een stijging van 500 euro leidt tot een stijging van 0.5 punt op de schaal van de levenstevredenheid. De vraag is dan in welke mate de levenstevredenheid stijgt als het inkomen verder stijgt van 2500 naar 3000 euro en verder naar 3500, 4000,…. Als de levenstevredenheid dan ook stijgt van 6.5 naar 7, en verder naar 7.5, 8,… dan kunnen we stellen dat de relatie tussen inkomen en levenstevredenheid proportioneel (lineair) is. De proporties van de stijging met het inkomen zijn immers gelijk.

Echter, dit is niet wat wordt vastgesteld. Naarmate het inkomen stijgt, stijgt de levenstevredenheid wel nog, maar in mindere mate. Het verband is dus niet proportioneel (lineair) maar iets anders. Om na te gaan of iets wel of niet lineair is kan men een kwadratische term toevoegen.

Als de coëfficiënt bij deze kwadratische term significant is (en in dit geval moet deze negatief zijn om te wijzen op de afnemende stijgingen), dan mag je inderdaad concluderen dat de relatie niet lineair is. Deze statistische significantie geeft dan uitsluitsel dat een kwadratische verband beter is dan een lineaire verband om het verband tussen inkomen en levenstevredenheid weer te geven.

Maar er zijn nog veel andere manieren om te testen of het verband lineair is of niet. Een kwadratische term toevoegen is er maar één van. Zo wordt in dit type onderzoek vaak ook een logaritmisch verband getest. In deze discussie is dat geen wiskundige haarkloverij, maar essentieel. Een kwadratisch verband met een negatief teken bij de kwadratisch term stelt een omgekeerde parabool voor. Dat betekent dat een kwadratisch verband stelt dat de levenstevredenheid bij hogere inkomens terug afneemt, na een maximum bereikt te hebben (= de top van de omgekeerde parabool). De logaritmische functie kent echter geen maximum: die blijft doorstijgen.

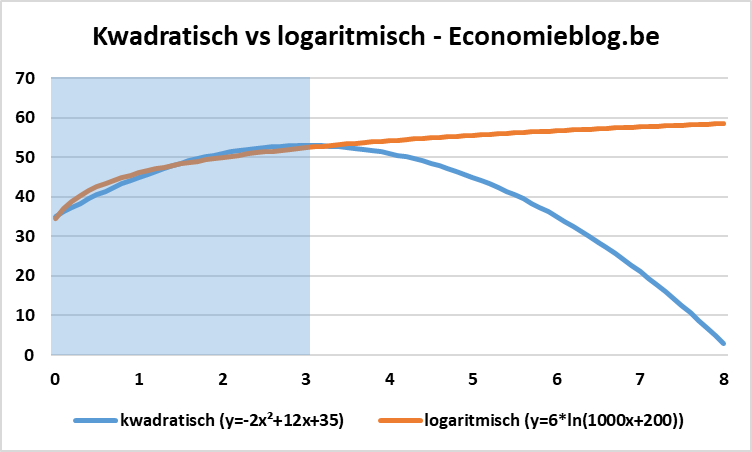
De blauwe lijn op de onderstaande figuur toont een kwadratische functie, waarbij het maximum zich op x=3 bevindt. De oranje lijn geeft de logaritmische functie. Deze lijn stijgt in het begin sneller dan op het einde, maar kent geen maximum. De lijn blijft doorstijgen, zij het heel traag.

Een logaritmisch verband geeft dus ook aan dat het verband tussen inkomen en levenstevredenheid niet lineair is (de stijging neemt af bij hogere inkomens), maar waar bij een kwadratisch verband de levenstevredenheid uiteindelijk terug moet afnemen, is dat niet het geval bij een logaritmisch verband. Bij een logaritmisch verband blijft de levenstevredenheid stijgen bij hogere inkomens, hoewel de stijging (veel) minder snel gaat dan bij lagere inkomens. En dat is net de conclusie van een ander onderzoek, van Stevenson en Wolfers uit 2013, namelijk dat er een logaritmische relatie is tussen inkomen en welzijn (“well-being”). De fout die in het Belgische onderzoek dan ook gemaakt is, is dat er op voorhand een bepaalde functionele vorm gekozen is, namelijk een kwadratische functie.

Als je bovenstaande grafiek bekijkt, dan lijkt het bijna onmogelijk dat je je kan vergissen tussen een kwadratisch of logaritmisch verband, omdat het verschil aan de rechterkant van de grafiek overduidelijk wordt. Maar dat verschil is er nagenoeg niet als je enkel de linkerkant van de grafiek bekijkt, met name het gedeelte met de blauwe achtergrond (tot x=3). Dan lijken de logaritmische en kwadratische functie sterk op elkaar.

En dat is net wat er aan de hand is met de gegevens van professor Annemans. In zijn onderzoek vallen bijna alle gegevens in het blauwe gedeelte. De maximale levenstevredenheid wordt immers pas bereikt tussen 4000 en 5000 euro, daarna zou deze afnemen. Maar daarna zijn er slechts een handvol gegevens. Als je enkel een kwadratische functie test met 99,8% van je gegevens die op of vóór het maximum van de kwadratische functie liggen, gelijkaardig aan de blauwe zone in de bovenstaande figuur, dan kan je geen uitsluitsel geven of het nu een kwadratisch of een logaritmisch verband is. Wil je dat wel kunnen, dan moet je veel meer gegevens hebben na de blauwe zone (en boven 5000 euro). Heb je die gegevens niet, dan kan je daar geen uitspraak over doen.

Ik heb deze analyse aan professor Annemans voorgelegd en hij erkende dat ze te snel gekozen hadden voor de kwadratische functie en dat ze ook de logaritmische relatie hadden moeten testen. Hij erkende dan ook dat ze de conclusie niet hadden mogen trekken dat levenstevredenheid afneemt bij hoge inkomens.

Op dat punt zijn we het dus eens en zou en het is belangrijk dat professor Annemans dit erkent. Hij stelde echter dat er geen gebrek aan data is om deze conclusie eventueel te kunnen trekken; er moet gewoon ook nog eens getest worden of de logaritmische functie beter is dan de kwadratische functie. Dat is volgens mij opnieuw een sterk betwijfelbare stelling. Meer nog, ik durf nu al te zeggen dat de data voor de zeer hoge inkomens veel te beperkt zijn om op een wetenschappelijk zinvolle manier uitsluitsel te geven tussen een logaritmische en kwadratische functie. Ik schat dat er immers maar 6 tot 9 datapunten in de inkomenscategorie van 5.000 euro en hoger zitten. Deze zullen geen statistische significante keuze kunnen maken tussen de kwadratische en de logaritmische functie. De enige wetenschappelijk aanvaarde conclusie moet zijn dat we op basis van de gegevens van professor Annemans niet kunnen weten of levenstevredenheid afneemt bij zeer hoge inkomens. Die conclusie is uiteraard minder sexy dan te kunnen stellen dat levenstevredenheid afneemt voor de hoogste inkomens, maar wetenschap is nu eenmaal niet altijd sexy (voor de media).

Tenzij ik iets over het hoofd zie, moet dit dan ook rechtgezet worden.

Meer uitleg over de kwadratische en logaritmische functies en een aantal simulaties vind je onderaan deze tekst.

Meer objectiviteit in plaats van meer subjectiviteit

Dat neemt niet weg dat de conclusie juist kán zijn dat de levenstevredenheid afneemt vanaf een zeer hoge inkomen. Maar zelfs als die conclusie correct zou zijn, dan nog is dat geen reden om ons economisch systeem te herdenken om het gelukniveau op te krikken. De reden is eenvoudig: geluk is subjectief. Er zijn mensen te vinden die arm zijn, maar veel gelukkiger dan de rijkeluiszoon die doodongelukkig is omdat hij geen Porsche kreeg voor zijn achttiende verjaardag. Om het geluksniveau dan op te krikken, zou je de arme meer moeten belasten om de Porsche van de rijke te betalen.

Het is een voorbeeld dat geïnspireerd is op het bekende artikel ‘Equality of What?’ van Amartya Sen uit 1979. Sen stelde zich de vraag wat we nu eigenlijk gelijk willen. Hij kwam tot de conclusie dat het niet om geluk (of nut) gaat. Sen stelde dat waar het om draait, is of mensen de mogelijkheid hebben om het goede leven te leiden. Daarvoor heb je een aantal basiscapaciteiten of -functies nodig. En die zaken kan je min of meer objectief vaststellen (hoewel ze in de tijd en tussen landen kunnen verschillen). Het gaat om basisbehoeften zoals voeding, wonen en veiligheid, maar ook over kunnen lezen en schrijven, politiek kunnen deelnemen en, in een maatschappij als de onze, toegang tot internet. Voor Sen is het duidelijk dat een maatschappij pas rechtvaardig is als deze objectieve noden voor elke mens vervuld kunnen worden. Of elke mens er ook daadwerkelijk gelukkig van wordt, is niet de verantwoordelijkheid van de maatschappij, maar van het individu zelf.

Tot slot, er is een andere reden waarom we hoge inkomens meer moeten belasten en lage inkomens minder. Er zijn drie oorzaken waarom mensen rijk zijn en die meestal samen in het spel zijn: erg rijke mensen werken vaak hard, hebben vaak ook veel talent en hebben ook gewoon geluk. Aan die twee laatste factoren heeft de rijke zelf geen verdienste, en daarom is het moreel aanvaardbaar dat we hogere inkomens meer belasten. Maar ook weer niet teveel, of rijke mensen gaan minder hard werken, waardoor je minder kan belasten en herverdelen. Er is dus ergens een optimum. Waar dit optimum ligt, is volgens mij een vraag voor de econoom die zich bezig houdt met de theorie van de optimale belastingstructuur. Voor het herdenken van ons economisch systeem hebben we dus eerder een ‘belastingseconoom’ dan een ‘gelukseconoom’.

BIJLAGE

Enkele simulaties over het kwadratische of logaritmische verband tussen levenstevredenheid en inkomen

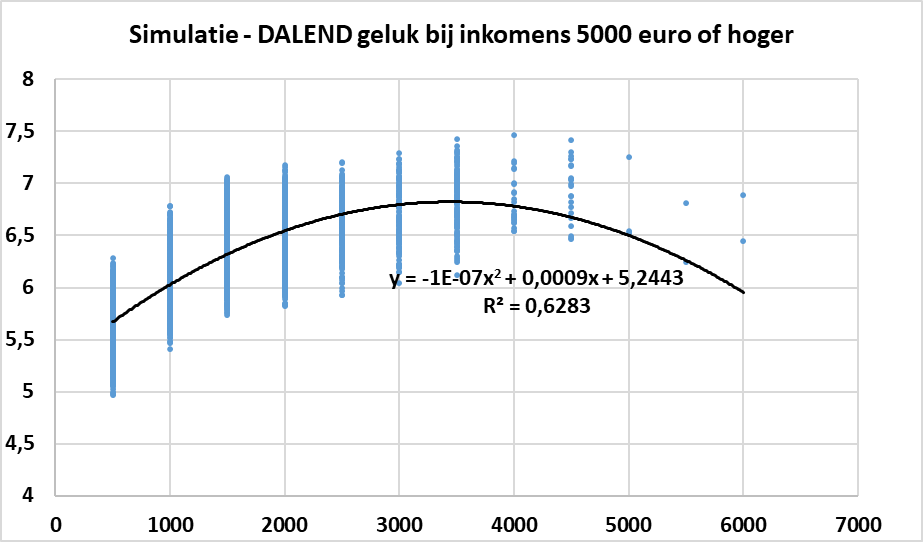
De onderstaande figuur simuleert de relatie tussen inkomen en levenstevredenheid, gegeven dat de laatste 7 datapunten (vanaf 5000 euro) effectief een dalende levenstevredenheid vertonen. In de simulatie is dan rekening gehouden met het aantal datapunten dat er beschikbaar was voor elk inkomensinterval. Het resultaat staat in de onderstaande figuur. Voor 500 euro gaat het om 777 datapunten, voor 1000 euro gaat het om 754, enzovoort. Voor 5000 euro gaat het om 3 datapunten, voor 5500 om 2 datapunten en voor 6000 of meer ook 2 datapunten. Ik heb wat ruis op de datapunten gezet.

Wanneer er een regressieanalyse wordt uitgevoerd op deze datapunten met als verklarende variabelen voor de levenstevredenheid het inkomen en het inkomen in het kwadraat, dan blijkt dat de coëfficiënt van de kwadratische term negatief is en dat dit resultaat zeer significant is.

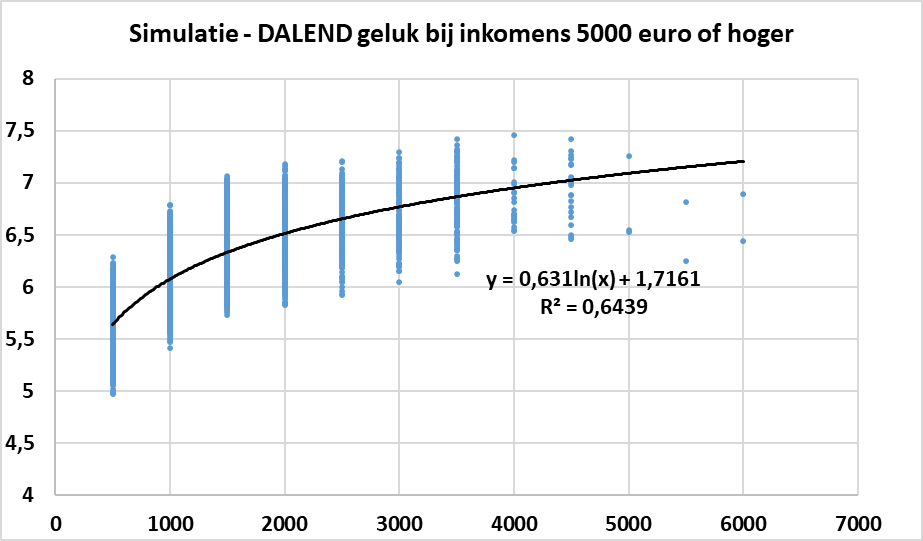
Je kan op dezelfde data echter ook een logaritmische relatie testen. De coëfficiënt bij de verklarende variabele is positief en ook dit resultaat is zeer significant (met p-waarde = 0). Bovendien blijkt de verklarende kracht van deze functionele vorm zelfs hoger te zijn: de R² voor een logaritmische relatie is 0.644 tegenover 0.628 bij de kwadratische vorm. Dit zou opmerkelijk moeten zijn, omdat we in deze simulatie aannemen dat de levenstevredenheid afneemt bij zeer hoge inkomens. Maar de 3300 datapunten tot 4000 euro volgen eerder een logaritmische functie en overstemmen de 7-8 datapunten van 5000 euro en hoger.

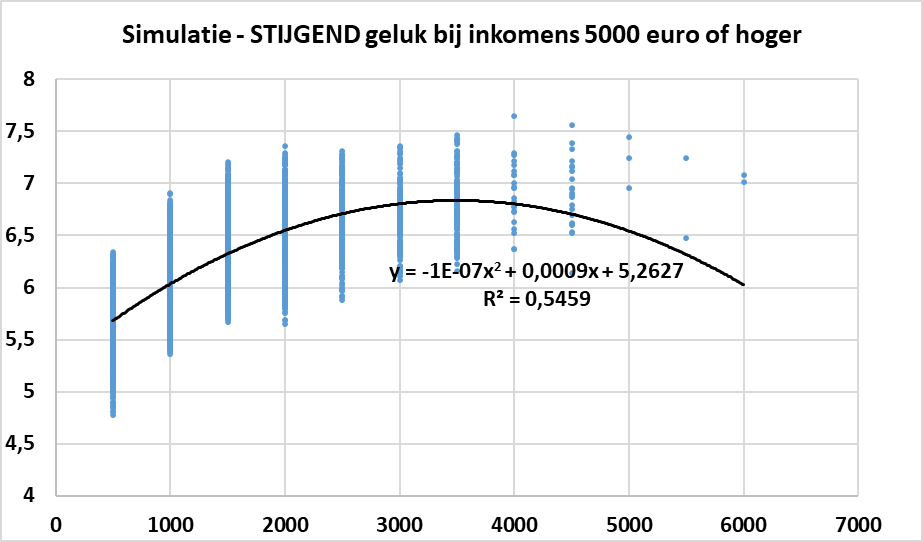
Ik heb ook eens dezelfde simulatie gedaan, maar voor de laatste 7 datapunten (vanaf 5000 euro) heb ik een stijging gesimuleerd: in deze wereld blijft de levenstevredenheid stijgen, ook bij grote inkomens. Met een regressieanalyse met de kwadratische vorm bekom ik opnieuw dat de coëfficiënt bij de kwadratische term significant negatief is.

Deze simulatie toont onweerlegbaar aan dat de conclusie die professor Annemans trekt niet kan getrokken worden op basis van zijn gegevens. De simulatie toont immers dat zelfs bij een sterk stijgende levenstevredenheid, ook bij zeer hoge inkomens, de conclusie van de statistische analyse is dat de coëfficiënt bij de kwadratische term negatief is, en dat dit zeer significant is.

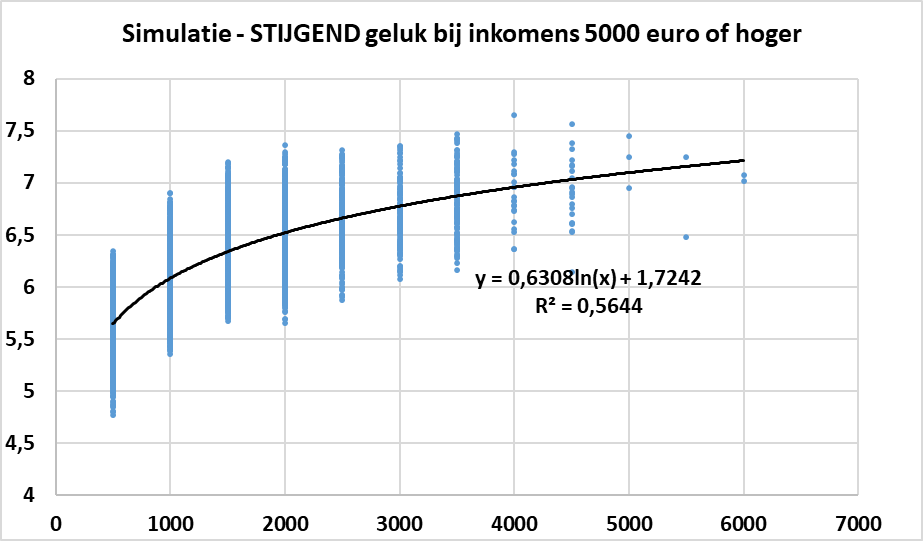
En natuurlijk kan je dit ook met een logaritmische vorm trachten te beschrijven, zoals in onderstaande figuur. De verklaringskracht van de logaritmische functie is -weinig verrassend- ook nu groter dan bij de kwadratische term.

De conclusie is volgens mij duidelijk: op basis van de gegevens die professor Annemans en zijn team verzameld hebben kan je niet zeggen dat de levenstevredenheid daalt bij zeer hoge inkomens.

Nationale Bank overdrijft Belgische gezondheidsuitgaven

Posted on July 13, 2017 by Andreas Tirez

Johan Swinnen, een bekend kankeronderzoeker van het UZ Leuven, stapt deze zomer te voet naar Compostela om geld in te zamelen voor de strijd tegen kanker. Bij zijn zoon Pieter werd zes jaar geleden een hersentumor ontdekt, toen hij 13 was. De Standaard deed vorig weekend een aangrijpend, maar tegelijk hartverwarmend interview met hen.

In dezelfde krant werd melding gemaakt van een studie van de Nationale Bank over de efficiëntie van de overheid. Dat zit volgens de Nationale Bank niet goed. Onder meer wat betreft gezondheidsuitgaven geeft België veel meer uit dan andere Europese landen zonder dat de kwaliteit erboven uitsteekt. Dat had Marcia De Wachter, directielid van de Nationale Bank, begin mei ook al verkondigd in Knack. Ze vergeleek de Belgische gezondheidsuitgaven met die in de buurlanden en de drie Scandinavische landen van de Europese Unie. “We geven pakweg 6 miljard euro teveel uit,” aldus De Wachter. Dat is zo’n 1,5 procent van het bruto binnenlands product (BBP).

Zes miljard is een fors bedrag. Het verraste me ook, omdat ik eerder al las dat België helemaal niet aan de kop zit wat betreft de uitgaven. Een snelle check met cijfers van de Oeso en Eurostat bevestigden mijn vermoedens: de cijfers van de Nationale Bank zijn hoogst merkwaardig en overschatten de Belgisch gezondheidsuitgaven (en die van Finland) en onderschatten de uitgaven onze buurlanden en van Zweden en Denenmarken.

De Nationale Bank baseert zich op cijfers van Eurostat. Ze berekent zelf de totale gezondheidsuitgaven door de uitgaven door de overheid (COFOG) en de gezinnen (COICOP) op te tellen.

Ik heb contact opgenomen met Eurostat om te vragen of de methode van de Nationale Bank kan toegepast worden. Eurostat antwoordde me dat ze daar niet op kunnen antwoorden, omdat dit geen officieel door Eurostat gebruikte methode is.

Meer nog, Eurostat meldde me dat in 2011 er internationaal een nieuwe methode werd opgesteld door Eurostat, de Oeso en de Wereldgezondheidsorganisatie dat resulteerde in the System of Health Accounts (SHA). Eurostat schrijft in hun mail het volgende:

“The SHA shares the goals of the system of national accounts (SNA): to constitute an integrated system of comprehensive, internally consistent, and internationally comparable accounts, which should as far as possible be compatible with other aggregated economic and social statistical systems.” (eigen onderlijning)

Eurostat publiceert met deze SHA-methode de totale gezondheidsuitgaven, die je dus internationaal kan vergelijken.

De Nationale Bank komt tot heel andere resultaten dan Eurostat, ook al baseert de Nationale Bank zich dus op cijfers van Eurostat. De oranje balkjes op de bijgaande grafiek geven voor 2014 de cijfers van Eurostat (SHA); de blauwe balkjes de cijfers van de Nationale Bank. Eurostat zet België in de middenmoot ten aanzien van de buurlanden en Scandinavische landen van de EU; Finland staat achteraan. De Nationale Bank zet België helemaal bovenaan, en Finland tweede.

Met deze bevindingen contacteerde ik de Nationale Bank. Ik vroeg hen of ze hun cijfers zouden aanpassen. Ze gaven toe dat hun methode mogelijks niet exhaustief was (“men kan niet uitsluiten dat sommige uitgaven niet opgenomen zijn”), maar verdedigden hun methode. Uit hun antwoord bleek dat de SHA-methode niet door de Nationale Bank gebruikt wordt.

Zij schreven onder meer het volgende: “Het grootste nadeel van deze alternatieve bron “SHA – System of Health Accounts” is dat de gegevens slechts tot 2014 beschikbaar zijn, met weinig historische gegevens.” Zo zijn de cijfers voor de periode 2000-2014 volgens Eurostat slechts beschikbaar voor drie landen.

Ik antwoordde hen dat hun reactie me nog meer overtuigde dat de Nationale Bank haar cijfers over de gezondheidsuitgaven moet aanpassen als ze een internationale vergelijking maakt. Het samentellen van COICOP en COFOG is niet verdedigbaar als de Nationale Bank tot een begrip wil komen van de ‘totale uitgaven’ en deze bovendien wil vergelijken met andere landen. Ik gaf daarvoor de volgende redenen:

1. Zoals de Nationale Bank zelf aanhaalt is de methode van de Nationale Bank mogelijks niet exhaustief (“men kan niet uitsluiten dat sommige uitgaven niet worden opgenomen”)

2. Eurostat heeft, na vier jaar werk, samen met de OECD en WHO in 2011 een nieuwe methode opgesteld om de gezondheidsuitgaven te berekenen. Uit de mail van de Nationale Bank kan ik opmaken dat de Nationale Bank deze cijfers niet gebruikt en mogelijks deze nieuwe methode nog niet kende. Eurostat schrijft zelf het volgende over het System of Health Accounts (SHA): “The SHA shares the goals of the system of national accounts (SNA): to constitute an integrated system of comprehensive, internally consistent, and internationally comparable accounts“ (eigen onderlijning) => voor internationale vergelijkingen moeten de SHA-cijfers gebruikt worden.

3. De voornaamste reden dat de Nationale Bank toch COICOP en COFOG wil gebruiken en niet SHA-cijfers is dat er onvoldoende data zijn om gemiddelden te nemen over de periode van 2000 tot 2014. Er zijn inderdaad niet van alle landen historische SHA-cijfers, omdat nog niet alle landen hun historische cijfers bijgewerkt hebben op basis van de nieuwe SHA-methode. Dat betekent simpelweg dat er nog geen betrouwbare, historische cijfers zijn voor alle landen en dat er dus gewoon geen cijfers kunnen gebruikt worden. Als reactie op het gebrek aan cijfers dan maar onbetrouwbare cijfers gebruiken kan natuurlijk niet. Overigens zijn voor 2014 SHA-cijfers voor alle landen gekend.

4. Er zijn wel al historische SHA-gegevens voor een aantal landen. België heeft SHA-cijfers sinds 2003 en ook Duitsland, Finland en Zweden hebben sinds minstens 2003 cijfers. De onderstaande tabel geeft de gemiddelde uitgaven voor de Nationale Bank-methode (COICOP+COFOG) en de SHA-Eurostat-methode voor 2003-2014 voor deze vier landen. De SHA-cijfers tonen dat de gemiddelde Belgische uitgaven voor deze periode lager liggen dan Duitsland en dicht bij die van Zweden, terwijl de Nationale Bank-cijfers heel andere conclusies geven (met een onderschatting van Duitse en Zweedse gezondheidsuitgaven en een overschatting van de Belgische en de Finse).

5. De methode van Nationale Bank leidt tot inconsistenties. Zo komt de Nationale Bank tot cijfers voor België en Finland voor 2014 die hoger liggen dan de SHA-cijfers (ook al zijn de Nationale Bank-cijfers mogelijks niet-exhaustief). De Nationale Bank zet Zweden dan weer 2,5 procentpunt onder de SHA-cijfers (zie tabel voor 2014). Dit is inconsistent.

6. De Nationale Bank schrijft zelf dat de cijfers van de gezondheidsuitgaven grondig zijn aangepast. Inderdaad, daarom was wellicht de vierjarige oefening door Eurostat, OECD en WHO inzake de SHA-cijfers noodzakelijk en leidde dit in 2011 tot de nieuwe methode van SHA.

Conclusie: op basis van wat Eurostat schrijft en op basis van de argumenten die de Nationale Bank zelf aanhaalt, is het duidelijk dat de methode van de Nationale Bank niet kan gebruikt worden. Tenzij de Nationale Bank zou kunnen aantonen dat de SHA-cijfers verkeerd zijn.

De discussie over deze verschillen in cijfers is niet onschuldig. De Nationale Bank stelt immers dat België ondanks de hoogste uitgaven niet de beste gezondheidszorg levert (gemeten volgens een door de Nationale Bank samengestelde index). Meer nog, zes Europese landen halen volgens de Nationale Bank een betere kwaliteit met –soms fors- minder middelen, waaronder Nederland, Zweden en Frankrijk. Grondige hervormingen en besparingen in de Belgische gezondheidszorg lijken dan onvermijdelijk.

De Nationale Bank berekende als reactie ook eens de efficiëntie met de cijfers van Eurostat. Dan blijken er slechts drie landen (Oostenrijk, Italië en Spanje) het beter te doen met minder middelen. Zweden, Frankrijk en Nederland leveren wel betere kwaliteit, maar deze landen geven met de nieuwe cijfers gevoelig meer uit aan gezondheidszorg dan België. Denemarken en Duitsland geven evenveel of meer uit, maar leveren een lagere kwaliteit.

Met andere woorden, met de nieuwe cijfers verandert het plaatje grondig. Dat neemt niet weg dat de Belgische gezondheidszorg efficiënter kan, maar België bungelt niet hopeloos achteraan. We zitten eerder in de subtop. En het kan zelfs zinnig zijn om de gezondheidsuitgaven te verhogen, samen met de hervormingen die bezig en gepland zijn.

De publieke en politieke discussie over de gezondheidsuitgaven is letterlijk van levensbelang. Het interview van professor Swinnen en zijn zoon illustreert dat. Gezondheidszorg gaat over ziekte, leven en dood, over mensen die kwetsbaar zijn en soms wanhopig op zoek naar een behandeling, wat ook de kostprijs is. Toch is er ook een budgettaire realiteit waarbinnen de zorgverstrekkers moeten werken. Er moeten vaak harde keuzes gemaakt worden. Dan zijn correcte cijfers onontbeerlijk.

Wanneer de Nationale Bank gezondheidsuitgaven internationaal vergelijkt, moet ze de internationaal gangbare methode gebruiken. Concreet betekent dit dat ze haar gezondheidsuitgaven moet aanpassen. Doet ze dat niet, dan schiet ze tekort in haar opdracht om de politiek en het publiek correct te informeren.

Deze tekst is een uitgebreide versie van de column die in De Tijd verscheen

Weddenschap wapent tegen vrijblijvende opinies

Posted on December 17, 2015 by Andreas Tirez

Meningen worden nauwkeuriger en beter gestoeld op feiten als je er weddenschappen over afsluit. En minder vrijblijvend.

In het publieke debat zijn opinies vaak te vrijblijvend. Opiniemakers en politici worden onvoldoende afgerekend op uitspraken die niet gehinderd worden door feiten. Soms zijn er echter niet genoeg data om goed geïnformeerd te discussiëren. Mensen vallen dan terug op hun eigen ervaringen en hun mens- en wereldbeeld.

Een voorbeeld is de terreurdreiging in Brussel na de aanslagen in Parijs, waarbij Brussel vier dagen lang een belegerde stad leek. Voor sommigen een totaal overdreven maatregel, voor anderen kon men niet voorzichtig genoeg zijn. Hoezeer iemands standpunt beïnvloed wordt door de persoonlijke situatie is moeilijk te bepalen.

Als je ver van Brussel woont en werkt, is het niet ondenkbaar dat je het gevaar minder sterk inschat dan als je elke dag het drukke, internationale treinstation Brussel Zuid moet passeren. De Brusselse pendelaar heeft er meer objectief belang bij dat de dreiging hoger wordt ingeschat dan de thuiswerker op het platteland.

De onterechte invloed van je situatie op je opinie kun je verminderen door een weddenschap aan te gaan over een mogelijke gebeurtenis. Ik zocht en vond een tegenpartij die met mij een weddenschap wilde aangaan over de terreurdreiging in Brussel. Mijn stelling is dat de kans dat een grote aanslag zoals in Parijs ook in Brussel kan gebeuren niet verwaarloosbaar is in 2016, terwijl dat volgens mijn tegenpartij wel zo is. Ik werk in Brussel, terwijl mijn tegenpartij veilig in een centrumstad blijft. De opbrengst werd na wat discussie vastgesteld op 10 euro als er geen grote aanslag zou plaatsvinden (ik zou dan moeten betalen), en 1.000 euro als dat wel het geval was (dan zou ik dat bedrag ontvangen).

Weddenschappen aangaan vermijdt niet alleen vrijblijvendheid, maar dwingt ook tot het nauwkeurig formuleren van de opinie, letterlijk tot na de komma. Zo werd het begrip ‘verwaarloosbaar’ gedefinieerd als ‘kleiner dan 1 procent’ (vandaar de ratio 10 tegen 1.000 euro). Om te kunnen vergelijken met de Parijse aanslag, werd een grote aanslag gedefinieerd als een aanslag met minstens 100 doden.

Die precieze informatie is eigenlijk altijd nodig als je wil begrijpen wat je gesprekspartner nu net bedoelt, maar er wordt in discussies zelden op ingegaan. Nu er een weddenschap is aangegaan, werd automatisch naar die informatie gevraagd om te weten welke voorwaarden je aanvaardt.

De weddenschap werd kenbaar gemaakt op Twitter. Ze stuitte echter al heel snel op protest. Mensen zagen er vooral een middel in om geld te verdienen op het al dan niet gebeuren van een aanslag zoals in Parijs, wat luguber overkomt. Die reactie is begrijpelijk, maar ze gaat voorbij aan het doel van de weddenschap: de vrijblijvendheid van opinies verminderen. En dat is juist nodig als het gaat om zulke belangrijke dingen als de terreurdreiging. Hoe luguber het ook mag lijken, het spelelement dat een weddenschap oproept, is hier niet de essentie. Bovendien acht ik de vrijblijvendheid van opinies schadelijker dan het lugubere karakter van de weddenschap.

Toch bedachten we de oplossing om de opbrengst van de weddenschap aan een goed doel te schenken, zodat we de beeldvorming konden tegengaan dat we geld wilden verdienen aan een mogelijke aanslag. Het nadeel is wel dat het veel moeilijker wordt om nog een tegenpartij te vinden, omdat je enkel kunt verliezen aan dergelijke weddenschappen.

Tot slot en in de marge: ik heb met Rik Van Cauwelaert, columnist van deze krant, een weddenschap lopen over de overheidsschuld. Een paar maanden geleden stelde ik dat de overheidsschuld geen 111 procent van het bruto binnenlands product is, zoals op Twitter beweerd werd, maar eerder 106 procent. Van Cauwelaert was sceptisch over mijn stelling, wat ik te vrijblijvend vond van hem. Hij was bereid tot een weddenschap: hij stelt dat de overheidsschuld eind dit jaar boven 108,5 procent uitkomt, en ik stel het omgekeerde. De inzet is maar een fles sterkedrank en een boek, maar ik kan niet wachten om ze in ontvangst te nemen!

De tekst verscheen eerst als column in De Tijd.

Financieringskosten België: meer data-analyse

Posted on March 9, 2014 by Andreas Tirez

In een vorige blogpost besprak ik de financieringskosten van België en de impact eind 2011 van de ‘Leterme-bons’ en de vorming van de regering Di Rupo. Volgens mij deden die twee gebeurtenissen de financieringskosten van de Belgische overheden dalen. Ik steunde me onder meer op een figuur van Peter Vanden Houte, hoofdeconoom bij ING, die hij toonde tijdens een presentatie en de bijbehorende uitleg: volgens hem veranderden die twee genoemde gebeurtenissen hoe de marktspelers de kredietwaardigheid van België evalueerden: die evolutie was positief waardoor de risicopremie die België moest betalen significant daalde.

Kurt Verstegen, een blogger en professioneel bezig met onderzoek over financiële markten, onderzocht mijn stelling kritisch: op basis van een statistische analyse zag hij geen factoren die specifiek voor België de financieringskost significant verlaagden. Hij schrijft in zijn conclusie onder meer dit:

Al bij al zijn de feiten dat één factor het grootste deel van de spreads drijft. En dat de claim dat de daling van onze financieringskosten vooral het resultaat is van goed werk van de regeringen daarmee een beetje in het water valt.

Data-analyse op een hoger niveau

Kurt gebruikt voor zijn analyse de techniek van principale componenten analyse. Het is een techniek die tracht de achterhalen of en in welke mate er een gemeenschappelijke factor is die de waargenomen variatie van verschillende variabelen kan verklaren. De verschillende variabelen zijn in deze oefening de rente die de verschillende landen moeten betalen op zijn schuld (of de spread met Duitsland).

De techniek is zowat het eerste wat je te leren krijgt bij multivariate statistiek, maar het is – althans wat mij betreft- data-analyse op een hoger niveau. Het gaat niet meer over het maken van een aantal grafieken of het berekenen van een aantal correlaties.

Ik ben van mening dat het geven en analyseren van cijfers het begin is van een maatschappelijke discussie, niet het einde ervan. En zij die deelnemen aan de discussie moeten bereid zijn cijfers proberen te interpreteren, ook al is dat niet altijd even gemakkelijk. Als de probleemstelling en de discussie geholpen worden door moeilijke(re) statistische technieken te gebruiken, dan moet dat gebeuren, ook al kost dat (heel) wat moeite.

Anderzijds is het zo dat ook moeilijkere statistische technieken niet noodzakelijk het correcte antwoord geven. En ook kritiek op deze methode kan nodig zijn. Hieronder ga ik de methode en de resultaten van de principale componenten analyse van Kurt behandelen.

Ik analyseer de rente, niet de spread met Duitsland. Ik weet niet of dat veel verschil maakt, maar Finland en Nederland lijken eveneens sterke risk free waarde te hebben (Frankrijk en Oostenrijk minder), waardoor de spreads in absolute waarde zeer weinig fluctueren, waardoor ik me afvraag of ze de resultaten niet vertekenen (maar dat weet ik dus niet).

1. 90% gemeenschappelijkheid kan veel verhullen

De techniek van de principale componenten analyse gebruikt als input de covariantiematrix van de variabelen. Hieronder toon ik de correlatiematrix van deze variabelen (correlaties zijn covarianties die genormaliseerd zijn door de standaarddeviaties met als resultaat een waarde tussen -1 en 1).

Als de gemeenschappelijkheid van België met de kernlanden wordt geanalyseerd, dan blijkt deze volgens Kurts analyse 90% te zijn. Heel veel variatie van België én de kernlanden wordt dus verklaard door één factor, en dat kan dus niet de regeringsvorming zijn of de Leterme-bons omdat dat specifiek voor België een impact zou gehad hebben en niet op de andere landen (men kan ook dat betwijfelen, maar laten we dat nu aannemen). De periode die Kurt analyseert is 2011 en 2012.

Echter, zoals te zien is op correlatiematrix, zijn de kernlanden sterker met elkaar gecorreleerd dan België. Misschien verklaart de gemeenschappelijke factor wel heel veel variatie van de kernlanden, maar minder van België, en veel minder van Spanje en Italië.

Dat wordt volgens mij ook bevestigd als je de factor loadings bekijkt van de eerste factor. Kurt heeft deze in een bijkomende analyse gepubliceerd (zie pagina 3 van dit document). Daaruit blijkt dat de “factor loadings” op de eerste component hoog zijn voor de kernlanden: tussen 0,402 (voor Frankrijk) en 0,557 (voor Finland). Voor België is deze 0,301, voor Italië 0,204.

Ik weet niet zeker of mijn kritiek op de principale componenten analyse klopt, maar bekijk het eens zo: stel dat er vijf landen zijn die exact hetzelfde patroon vertonen: bij deze landen zal een principale componenten analyse alle variatie verklaren door één factor. Als je er dan één land bijvoegt dat een ander patroon volgt dan die vijf landen, dan zal de principale componenten analyse nog steeds concluderen dat één factor veel variatie verklaart. En als dat bijgevoegde land in een bepaald periode niet hetzelfde patroon volgt en tijdens een andere periode wél, dan zal de verklaringskracht van die ene factor nog stijgen.

2. Voor en na BeGov

De principale componenten analyse wordt dus toegepast op de hele tijdsreeks, waarmee ik bedoel zowel voor als na de regeringsvorming. Het punt is echter dat er volgens mij een breuk in de tijd is: de figuur met de rentes (of de risicopremie), die ik hieronder herneem voor de beschouwde periode, lijkt te suggereren dat België vóór de regeringsvorming eerder bij de perifere landen zoals Italië en Spanje gerekend werd, terwijl België na de regeringsvorming (zeker na verloop van tijd) naar de kernlanden opschuift.

Hieronder geef ik dezelfde correlatiematrix als hierboven, maar dan één voor de periode vóór de regeringsvorming (van 1 januari 2011 tot 6 december 2011) en één na de regeringsvorming (van 7 december 2011 tot 31 december 2012).

Vóór de regeringsvorming is de correlatie van België met de kernlanden laag, soms zelfs licht negatief. Italië en Spanje hebben lage positieve tot grote negatieve correlaties met de kernladen. Duitsland, Nederland en Finland lijken echt de kern te vormen; Oostenerijk en Frankrijk zitten er kort tegen, maar vormen toch een groepje apart.

Na de regeringsvorming verandert dit beeld compleet: België komt nu in het groepje van Oostenrijk en Frankrijk dat zelf meer tot de kernlanden lijkt te gaan behoren.

Ook de correlatie van Italië met de kernlanden Duitsland, Finland en Nederland verandert sterk: van sterk negatief (rond -0,7) naar gematigd positief (rond +0,35).

De onderstaande figuur vat de cijfers uit de twee bovenstaande correlatiematrices samen voor wat betreft België. De correlatie van België met de kernlanden vóór de regeringsvorming wordt gegeven door de blauwe balkjes: correlatie is laag tot zelfs negatief. Na de regeringsvorming (rode balkjes) is deze zeer hoog: de verandering is spectaculair te noemen.

Omgekeerd verandert de correlatie met Spanje sterk: vóór de regeringsvorming is deze hoog, erna wordt deze negatief. Enkel de correlatie van België met Italië is het op eerste gezicht vreemd: deze blijft min of meer gelijk.

3. Italië en België: een gelijkaardige politieke evolutie?

Het patroon van Italië is speciaal: voor en na de Belgische regeringsvorming blijkt ook het patroon van de Italiaanse rente sterk te veranderen, namelijk eerst een sterk negatieve correlatie met de kernlanden, die na de Belgische regeringsvorming gematigd positief is. Di Rupo mag dan al Italiaanse roots hebben, maar een dergelijke impact kunnen we niet toeschrijven aan de Belgische regeringsvorming.

[Hoewel ook dat kan betwijfeld worden: de financiële wereld is sterk verbonden met elkaar. Dat heeft het bankroet Lehman Brothers, dat de hele financiële wereld op haar grondvesten deed daveren, duidelijk aangetoond. En ook een eventueel ongecontroleerd Grieks bankroet deed de hele eurozone beven. Het is dan ook niet onzinnig om te veronderstellen dat een verhoogd risico op een Belgische wanbetaling ook andere (Europese) landen in problemen kan brengen, met verhoogde rentes tot gevolg.]

Er is in die periode echter ook iets belangrijk gebeurd in de Italiaanse politiek: Berlusconi nam ontslag als premier op 12 november 2011 en werd een paar dagen later vervangen door Mario Monti, iemand die uit de financiële wereld komt en het vertrouwen genoot van de spelers op deze markt. Met andere woorden, het gevaar op politieke instabiliteit in Italië verminderde wellicht sterk in november 2011 en de tijd erna.

Conclusie

Volgens mij moet er dus een analyse gemaakt worden voor en na de federale regeringsvorming. Als Kurt met een dergelijke analyse komt die statistisch aantoont dat er geen significant verschil is tussen voor en na de regeringsvorming, of dat het verschil wel significant is maar dat de impact klein is, dan zal ik dat kritisch bekijken. Als ik geen argumenten vind om dat te ontkrachten, dan zal ik mijn stelling daaraan aanpassen.

Tevens denk ik dat het patroon van Italië eerder de stelling versterkt dat politieke (in)stabiliteit een impact heeft (of tenminste had) op de rente die een overheid op de schuld moet betalen.

En een meta-conclusie: dit is het soort debat dat ik graag meer wil voeren: over cijfers en de analyse ervan. Dat kan je natuurlijk niet alleen, maar Twitter en blogs lenen zich perfect voor dit soort discussies. En bij deze dus een volgtip voor Kurt Verstegen.

Foute data stellen België in verkeerd daglicht

Posted on February 16, 2014 by Andreas Tirez

Op Twitter doet onderstaande figuur al een paar maanden de ronde. Vooral @Gelerobbie, een ondernemer die zich “lid van de oppositie” noemt, heeft deze figuur al meerdere keren getweet. En een zekere @Kristof_A heeft het zelfs als achtergrond bij zijn Twitter-bio.

De figuur werd getoond op een studiedag van de N-VA in oktober 2013. De auteur van de figuur is Mathieu Isenbaert, een specialist tax law, verbonden aan HUB en KUL (met dank aan @Gelerobbie en @lvandingenen voor het speurwerk).

De figuur toont een sterke stijging van de overheidsinkomsten als percentage van het BNP (voor de meeste landen, en ook voor België, maakt het niet veel uit of je BNP of BBP gebuikt; voor Ierland is dat iets anders). Door dit uit te drukken als percentage van het BNP, worden de overheidsinkomsten dus gecorrigeerd voor inflatie en economische groei. En dat is zoals het dus moet (en waar ik zelf al meermaals op gehamerd heb, zie dit bijvoorbeeld dit drieluik: deel 1, deel 2 en deel 3).

Dus ondanks de correctie voor inflatie en economische groei, noteert België een forse stijging van de overheidsinkomsten: van minder dan 40% in 1995 tot boven 50% in 2012. Boeken toe, dus, voor de verdedigers, waaronder ikzelf, van de stelling dat België het nog zo slecht niet doet.

Alleen klopt de figuur niet. Er wordt namelijk een zware fout gemaakt in de berekening van de overheidsinkomsten als percentage van het BNP: in de teller worden de nominale overheidsinkomsten gebruikt, terwijl in de noemer het reële BNP gebruikt wordt. De overheidsinkomsten zijn dus niet gecorrigeerd voor inflatie, terwijl het BNP wel wordt gecorrigeerd (in euro’s van 2010).

De onderstaande figuur toont de correcte gegevens. Dat oogt al veel minder spectaculair. Er is in 2012 een stijging van de overheidsinkomsten tot 50,9%, maar dat zit maar een paar procentpunten boven het laagste niveau van de periode 1995-2012 en slechts 0,2 procentpunt boven het niveau van 2003: de overheidsinkomsten schommelden de afgelopen 18 jaar tussen 47,5% en 50,9%. Dat is dus best wel opmerkelijk, gezien België (en de rest van Europa) nu al het vijfde crisisjaar op rij telt. Het wordt wel eens vergeten, maar we moeten al terug gaan tot de jaren ’30 voor een dergelijke crisis. Van uitzonderlijke omstandigheden gesproken…

De figuur hieronder toont welke fout gemaakt is. De grijze lijn geeft de nominale overheidsinkomsten (dus niet gecorrigeerd voor inflatie). De blauwe lijn geeft het reëel BNP (gecorrigeerd voor inflatie, met als referentiejaar 2010) en de rode lijn geeft het nominaal BBP.

Doordat het BNP gecorrigeerd wordt voor inflatie is de economische activiteit in de jaren vóór het referentiejaar 2010 hoger dan het nominale BBP; na het referentiejaar is dat kleiner. Het is het reële BNP die door Isenbaert in de noemer gezet wordt, terwijl de nominale ontvangsten in de teller komen. Een hoger BNP in noemer betekent dus ook een lager resultaat als uitkomst. En hoe verder je in de tijd teruggaat, hoe groter de fout is. Maar ook hoe groter de totale stijging lijkt.

Het lijkt me meer dan waarschijnlijk dat Mathieu Isenbaert hier onbewust een fout gemaakt heeft. Zijn specialiteit is tax law, niet macro-economie. Bovendien maakt iedereen wel eens een fout (zeker als je met data werkt!). Het gevolg van deze fout is wel dat het beeld bevestigd wordt dat België volledig de verkeerde kant opgaat. Misschien helpt het als @Gelerobbie de correcte figuur tot vervelens toe rondtweet. Dank bij voorbaat!

We leven in een geweldige tijd

Posted on December 29, 2013 by Andreas Tirez

Eind november hield Open VLD haar toekomstcongres. De tekst die goedgekeurd werd, begint met “We leven in een geweldige tijd”. Als liberaal dacht ik: eindelijk, eindelijk iemand die erkent wat we allemaal zouden moeten erkennen: ja, het gaat goed, het gaat zelfs geweldig goed. We zijn rijker, gezonder en welvarender dan ooit tevoren. Combineer dat met de individuele onvervreemdbare basisvrijheden die we hebben in een liberale democratie en iedereen die genoeg kansen krijgt, kan iets geweldigs van zijn of haar leven maken.

Maar de slogan is durven. Het gaat immers volledig in tegen de tijdsgeest. De grote meerderheid denkt dat de jongere generatie het slechter zal hebben. Hieronder een grafiek uit een enquête van het ILO, de internationale vakbond. 87% van de Belgen antwoordde “slechter” op de vraag of de toekomstige generaties het beter of slechter zullen hebben. Het pessimisme is wijd verspreid maar in België toch ruim boven het gemiddelde van 66%.

In een interview in De Tijd lijken Etienne Vermeersch en Tinneke Beeckman ook tot het kamp van de doemdenkers te behoren. Een citaat van Vermeersch:

Onze economie is een piramidespel. Dat zinnetje zou elke dag in hoofdletters op de voorpagina van uw krant moeten staan. In een piramidespel overhalen deelnemers anderen om mee te doen, waarbij de bijdrage van de nieuwkomers wordt uitbetaald aan de vorige deelnemers. Dat systeem werkt. Iedereen wint, op voorwaarde dat er telkens meer deelnemers bijkomen, die zorgen dat er meer kan worden geproduceerd, zodat vervolgens meer kan worden geconsumeerd. Maar de piramide kan zich niet oneindig uitbreiden. Het systeem teert op grondstoffen die in snel tempo op geraken. Het produceert afval, maar de afvalbakken – bodem, rivieren, zeeën en lucht – lopen vol. Dat piramidespel stort ineen tegen het einde van deze eeuw. Misschien vroeger al.

Onze economie is een piramidespel. En voorlopig werkt het. Dat laatste klopt alvast. Hieronder het BBP per hoofd van de bevolking in België en de EU-27 en EU-15 (in reële termen – euro’s van 2005). Ondanks de huidige crisis, de diepste sinds de jaren ’30, zijn we in 2013 niet of nauwelijks armer dan vóór de crisis.

Op basis van bovenstaande grafiek kan niemand ontkennen dat we in een geweldige tijd leven. Maar Vermeersch gaat verder: “Het systeem teert op de grondstoffen die in snel tempo op geraken. Het produceert afval, maar de afvalbakken -bodem, rivieren, zeeën en lucht- lopen vol.”

Wel, is dat zo? Opinions are cheap, facts are expensive. Dus waarom niet wat feiten erbij halen. Hieronder een aantal grafieken van de Studiedienst van de Vlaamse Regering. Ik heb ze gehaald uit de sectie ‘Mileu&natuur’. Het is een selectie waarbij ik vooral gekeken heb naar de lengte van de tijdsreeks (hoe langer, hoe beter, volgens mij). Alle gegevens staan in aparte excel-files en ik heb er tien van gedownload.

1. Huishoudelijk afval per capita: stijging in de jaren ’90, lichte afname sinds 2000. Sterke stijging evenwel van het gesorteerde afval, en navenant sterke daling van het niet-gesorteerde afval. Mijn oordeel: gaat in goede richting.

2. Zware metalen in in oppervlaktewater: overal sterke daling sinds 2000, behalve voor arseen waar we terug bijna op niveau van 2000 zitten. Mijn oordeel: sterke verbetering.

3. Evolutie bosgezondheid: sterke stijging van beschadigde bomen in Vlaanderen tot 1995, daarna lichte daling en laatste twee jaren terug sterke stijging. Mijn oordeel: hoewel het al slechter is geweest, gaat het niet de goede kant op.

4. Er is veel te doen rond fijn stof, daarom toch deze grafiek, hoewel beperkte tijdsreeks (2004-2008): aantal verloren gezonde levensjaren door fijn stof: lichte daling. Mijn oordeel: gaat goede kant op.

5. Dioxine-emissies: spectaculaire daling sinds jaren ’90. Mijn oordeel: gaat goede kant uit.

6. Emissie poly-aromatische koolwaterstoffen: sterke daling sinds 1990, maar stijging ten opzichte van 1995. Mijn oordeel: gaat slechte kant uit, maar niet dramatisch.

7. Potentieel verzurende emissies: sterk en blijvende daling sinds jaren ’90. Mijn oordeel: gaat goede kant ui.

8. Evolutie biologische kwaliteit van het oppervlaktewater: sinds begin jaren 90 sterke vermindering van ‘slechte’ kwaliteit. Veel ‘slechte’ kwaliteit lijkt ontoereikend’ geworden, maar toch ook sterke relatieve stijging van ‘matig’, ‘goed’, ‘goed en hoger’ en ‘zeer goed’. Mijn oordeel: gaat goede kant op.

9. Bodem-verontreiniging: sinds 2000 stijging van aantal te saneren gronden. Aantal onderzochte gronden stijgt eveneens, en aantal waar ‘beschrijvend onderzoek nodig’ is daalt licht. Interessante te weten: op 1 juni 2008 ging het nieuwe bodemdecreet in voege en wijzigde de definitie van ‘verontreinigde grond’. Ik veronderstel een verstrenging van de definitie. Mijn oordeel: matig negatief.

10. Verzuring-vermesting van natuur: dalingen van verzuring en vermesting, maar nog steeds boven normen voor 2015 (data lopen tot 2010). Mijn oordeel: gaat goede kant op.

Samenvattend: althans voor Vlaanderen lijkt het overwegend de goede kant op te gaan. Dat is op zijn minst opmerkelijk, aangezien Vlaanderen dicht bevolkt is met veel verkeer en nog steeds heel wat industrie.

Ik ben er mij bewust van dat deze overwegend positieve evoluties er niet vanzelf gekomen zijn: de maatregelen die de overheid genomen heeft, hebben gewerkt. Maar dat moet ons optimistisch stemmen: als we willen, kunnen we blijkbaar de problemen aanpakken. Dat zou de voornaamste boodschap moeten zijn: we kunnen welvarender worden én het milieu minder belasten. Dat hebben we de laatste 20 jaar bewezen.

We leven dus in een geweldige tijd, met enorme mogelijkheden. Welvarend, kansrijk (toch voor ongeveer 85% van de bevolking), in goede gezondheid, met individuele, onvervreemdbare rechten. En niets wijst erop dat dit niet zo gaat blijven duren. Meer nog, met ons milieu gaat het overwegend de goede kant op en we worden zeer waarschijnlijk in de toekomst met zijn allen nog rijker. Innovatie staat niet stil.

Pessimistic bias

Bryan Caplan, een Amerikaans econoom, spreekt van een ‘pessimistic bias’: “a tendency to overestimate the severity of economic problems and underestimate the (recent) past, present, and future performance of the economy.” Ik denk dat dit wel kan kloppen. Een voorbeeld: toen ik twee jaar geleden over de zelfrijdende auto sprak, kreeg ik enkel meewarige blikken. Nu al veel minder; en binnen minder dan tien jaar is het misschien realiteit.

Van waar komt dan toch dat pessimisme? Ik weet het eigenlijk niet. De eenvoudigste verklaring is dat ‘doemdenken’ ernstig klinkt, en wie wil er niet ernstig genomen worden? Ook risico-aversie kan veel verklaren: “het moet maar eens waar zijn”. Maar dat is speculatief.

Het enige waar ik zelf niet zo optimistisch over ben, is klimaatopwarming. Ik ben absoluut geen klimaatexpert, maar wat ik wel weet is dat dit een globaal probleem is. Misschien gaat de Europese Unie haar doelstellingen wel halen, maar China doet dat met gemak teniet. Ik denk dat enkel technologische innovatie hier een oplossing kan bieden, en dat is natuurlijk onzeker.

Kunst en het maatschappelijke debat

Posted on May 17, 2013 by Andreas Tirez

Peter Casteels, columnist bij Apache, schreef een opmerkelijke blog over cultuursubsidies. Hij reageert op mijn stelling dat er geen bewijs lijkt te zijn dat cultuur positieve externaliteiten heeft en dus ook geen subsidies zou mogen krijgen. Casteels reageert ook op de volgens mij uitstekende blogpost van Kurt Verstegen die het allemaal iets plastischer uitlegt aan de hand van lelijke broeken. Ik vind de blog van Casteels opmerkelijk, omdat hij voorstander is van cultuursubsidies en ten gronde reageert op de kritiek dat cultuur geen positieve externaliteiten oplevert en dus geen subsidies mag krijgen. Het is de beste verdediging voor cultuursubsidies die ik tot nu toe gelezen heb.

Casteels lijkt te zeggen dat de voornaamste positieve externaliteiten van cultuur liggen in de meerwaarde dat cultuur levert voor het maatschappelijke debat, met een verwijzing naar universiteiten. Of eerder zou kunnen leveren. Want op dit moment doet cultuur dat niet. Ik citeer hem over theater:

Het enige theater waarvan ik mij herinner dat de inhoud ook buiten de zalen werd besproken, was geschreven door Tom Lanoye.

Uit mijn ervaring als theaterbezoeker – louter anekdotisch, waarvoor excuses – kan ik getuigen dat die weinige aandacht terecht is. De intellectuele kwaliteit van het meeste theater is zodanig pover dat het best genegeerd wordt in het publieke debat.

En hij gaat nog een stapje verder door hiervoor de schuld juist bij de subsidies te leggen:

Ik denk – met tegenzin – dat de reden hiervoor de overmatige subsidiëring door de overheid is. Makers hoeven – kort door de bocht – enkel verantwoording aan elkaar af te leggen, waardoor een milieu kon ontstaan dat losstaat van de werkelijkheid.

Theater zit dus met een probleem dat ze niet maatschappelijk relevant moet zijn, omdat ze toch gesubsidieerd is. Daardoor kunnen ze lekker onder zichzelf wat aanmodderen en heeft de rest van de goegemeente er niets aan waardoor je eigenlijk de subsidies zou moeten afschaffen, want geen maatschappelijke meerwaarde.

Het lijkt me een juiste analyse: als je echt geïnteresseerd bent in hoe mensen zijn en samenleven, en hoe je dat zou kunnen verbeteren, dan moet je volgens mij niet naar theater gaan of naar een museum (ja, ik heb het geprobeerd). Als je dat wil weten, dan lees je wetenschappelijke studies en boeken (vooral non-fictie, maar sommige fictie is nuttig om de empathie te trainen, wat mij broodnodig lijkt als je regels wil bedenken die de samenleving ook voor anderen beter zouden moeten maken). En dan ga je op zoek naar gegevens om bepaalde stellingen te onderbouwen, of nog beter, ze te weerleggen.

En ik vermoed dat theatermensen en cultuurwerkers dat net niet doen. Ik vermoed dat ze niet weten hoe ons belastingsysteem werkt, of wat de argumenten zijn voor het verplichtende karakter van onze sociale zekerheid, laat staan dat ze ook maar iets kennen van hoe financiële markten werken. Ook al leven we in financial times. Ik geef maar wat voorbeelden. (En daarmee wil ik niet zeggen dat je alleen maar mag deelnemen aan gelijk welk publiek debat op voorwaarde dat je iets kent van financiële markten; wat ik wil zeggen is dat er (momenteel) heel wat thema’s zijn in het publieke debat die daarvan enige kennis vereisen.)

Casteels zegt vervolgens dat het voorbeeld van de universiteiten ook niet lang meer zou kunnen gelden, omdat universiteiten meer en meer gedomineerd worden door het marktdenken. Dat kan kloppen, maar het is alvast niet wat ik bepleit voor de cultuursector. Meer nog, ik vind niet dat cultuur hun marktwaarde moet aantonen voor subsidies, maar wel hun maatschappelijke meerwaarde (positieve externaliteiten). En dat geldt ook voor universiteiten, die dat overigens aantoonbaar doen, onder meer -maar niet alleen- door deel te nemen aan het maatschappelijke debat. Daar vind je talloze voorbeelden van, zoals vandaag nog in De Morgen met een naar mijn mening sterke opinietekst van Wim Van Lancker over een maatschappelijk thema dat zeer relevant is.

Casteels eindigt met bescheidenheid in het weten.

Theatermakers en kunstenaars zullen zich moeten heruitvinden als ze willen blijven rekenen op de steun van de samenleving. Het cultuurbeleid van de overheid moet daarvoor veranderen. Zodat niemand het zich in zijn hoofd haalt theater te vergelijken met lelijke broeken. Ik weet alleen niet hoe.

Mijn voorstel: alle cultuurwerkers terug naar de universiteit, voor een master Economische Wetenschappen. Dan kunnen ze meediscussiëren over dingen zoals dit. Dat gaat theater geven.

Niet weten wat een logaritme is, daar loop je mee te koop

Posted on May 3, 2013 by Andreas Tirez

De Morgen pakte er gisteren mee uit op de voorpagina: 22% van de jongeren onder de 25 jaar is werkloos. En opvallend, uit de cijfers van de VDAB is de stijging op jaarbasis met 12,8% het grootst onder de hoogopgeleiden. De werkloosheid bij de hoogopgeleide jongeren steeg zelfs met 17,8%. Het zou sommigen ertoe kunnen verleiden om het almaar toenemende aantal hoogopgeleiden met de vinger te wijzen: in totaal is bijna 30% van de bevolking hoogopgeleid, en misschien is dat wat te veel van het goede.

Maar meer gedetailleerde cijfers geven een ander beeld: de situatie voor de hoogopgeleide is nog steeds veel rooskleuriger dan voor de laagopgeleide, ook wat de jongeren betreft. Van de 211.000 werklozen in Vlaanderen in maart 2013 is bijna de helft laagopgeleid, tegenover 15% hoogopgeleid. Indien we enkel naar de jongeren kijken, dan is 11% van alle Vlaamse werklozen een laagopgeleide jongere, tegenover nog geen 2% een hoogopgeleide jongere. Er zijn dus nog steeds veel meer laagopgeleide jongeren. De grote relatieve stijging van de werkloze hoogopgeleiden is te verklaren doordat deze categorie van een relatief lage basis vertrekt: in totaal kwamen er in een jaar 578 hoogopgeleide werkloze jongeren bij, waardoor deze categorie aanzwol tot net geen 4.000 werklozen.

STEM

De absolute aantallen zijn relatief laag. Toch kan het zijn dat we ons zorgen moeten maken, niet zozeer over het aantal hoogopgeleiden, als wel over de afstemming van vraag en aanbod. Het is immers al langer bekend dat er een gebrek is aan een bepaalde categorie opgeleiden, namelijk de zogenaamde STEM-opgeleiden: Science, Technology, Engineering & Mathematics. Het gaat om ingenieurs, wiskundigen en andere ‘harde’ wetenschappers, die veel wiskunde en cijfers in hun opleiding moeten verwerken.

Dat is het puur economische argument voor meer STEM-profielen: de economie heeft ze nodig. Er is volgens mij echter nog een maatschappelijk argument. Cijfers regeren de wereld, of zouden dat moeten doen. Of het nu gaat om het bouwen van een brug of het verbeteren van ons onderwijssysteem: zonder cijfers en goede statistiek vaar je blind en regeert het buikgevoel, wat veelal een synoniem is voor willekeur.

Meer STEM-opgeleiden betekent meer aandacht voor cijfers, ook in het democratische beslissingsproces. Media en politiek zijn nu gedomineerd door hoogopgeleiden die geen of weinig cijfers in hun opleiding hebben gezien. De aandacht voor cijfers en goede statistiek is volgens mij ondermaats. Meer nog, vaak wordt het gebruik van cijfers weggewuifd met de dooddoener dat je met cijfers alles kunt bewijzen.

Die dooddoener is tot op zekere hoogte correct: cijfers kúnnen misbruikt worden. De stijgende werkloosheid onder jonge hoogopgeleiden is een treffende illustratie: de grote relatieve stijging van de werkloosheid onder de hoogopgeleide jongeren kan een aanleiding zijn om te spreken van een verzadiging van de arbeidsmarkt voor hoogopgeleiden. Maar iedereen die een basisopleiding statistiek heeft gehad, zal onmiddellijk de absolute cijfers willen zien vooraleer conclusies te trekken.

Meer hoogopgeleiden – die grotendeels het publieke debat volgen en bepalen – die een begrip hebben van cijfers en goede statistiek zouden dergelijk misbruik gemakkelijker kunnen doorprikken. Met andere woorden, doordat er te weinig cijfergeletterdheid is, is het al te vaak zo dat je met cijfers alles kunt bewijzen. Meer cijfergeletterdheid zal leiden tot een kritische houding en een beter debat over cijfers. En wees gerust: ook mét cijfers is er nog veel ruimte voor ideologie en ethiek.

Je kunt natuurlijk jongeren niet dwingen om plots massaal een STEM-opleiding te gaan volgen. Jongeren moeten in de eerste plaats kiezen voor een richting die hen boeit. Maar hun omgeving is daarbij ook een bepalende factor voor die keuze. En ik kan me niet van de indruk ontdoen dat een goed begrip van cijfers te veel als saai wordt gezien. Om het met een boutade te zeggen: niet weten wie Shakespeare is, is beschamend; niet weten wat een logaritme is, daar loop je mee te koop.

Aan alle jongeren die eraan denken een STEM-opleiding te volgen, zou ik dan ook Nate Silver als voorbeeld willen suggereren: deze über-geek is in de VS een nationale bekendheid geworden omdat hij de winnaar van de laatste twee presidentsverkiezingen voorspelde. In 2012 had hij daarenboven ook nog eens 50 van 50 staten correct voorspeld. Hij deed het daarmee beter dan veel gerenommeerde experten en peilingbureaus. Zijn kracht: publiek beschikbare cijfers en goede statistiek.

Deze tekst verscheen eerst bij De Morgen.

Update: deze bevraging bij een 1000-tal Britten geeft wat data die de opinie in bovenstaande tekst ondersteunt. Vooral vraag Q1b is veelzeggend:

Stijgende misleidende overheidsuitgaven – deel 3

Posted on April 7, 2013 by Andreas Tirez

Zie hier voor deel 1 en deel 2.

Ivan Van de Cloot heeft gereageerd (Update: link werkt niet meer) op het feit dat ik stel dat het gebruik van nominale cijfers misleidend is als je de stijging van overheidsuitgaven van landen met elkaar wil vergelijken. Ik stel dat je de nominale cijfers moet corrigeren voor inflatie en economische groei.

In deze blogpost schrijf ik hierop een reactie, waarbij ik me focus op de cijfers die Van de Cloot gebruikt. De discussie aanzwengelen over cijfers is zowat de bedoeling van deze blog. Dat deze blogpost al de derde tekst is over dit specifieke onderwerp bekijk ik dan ook als een succesje…

In de blogpost van Van de Cloot worden twee figuren getoond met de stijging van de overheidsuitgaven (2012 ten opzichte van 2007), waarbij België telkens als grootste stijger uitkomt. De eerste figuur toont de procentuele verandering van de nominale overheidsuitgaven van 12 landen en de Euro12; de tweede figuur uit de blogpost geeft de reële cijfers met het gebruik van de HICP als deflator, nu van 13 landen en de Euro12. De selectie van landen bestaat uit eurolanden, de UK en de VS.

Van de Cloot toont geen figuur met overheidsuitgaven gemeten als aandeel van het BBP, wat volgens mij moet, maar zegt wel dat hij een dergelijke figuur toont in de pdf waar hij naar linkt. Hij schrijft: “Uiteraard kan het ook nog interessant zijn om naar de wijziging van de overheidsuitgaven te kijken als % van het bbp. Dit doe ik ook in de nota waarvan de link verder wordt meegegeven.” Ik denk dat hij grafiek 5 bedoelt uit de pdf.

Ik heb een aantal opmerkingen op het gebruik van de cijfers, zowel met de twee figuren uit de blogpost als met grafiek 5 uit de pdf (als het die figuur is die bedoeld wordt). Ik behandel ze hieronder.

De eerste figuur geeft 12 landen en de euro12, dertien in totaal. De tweede figuur geeft 13 landen en de euro 12. Het land dat mankeert op de eerste figuur is Finland. Ik geef dezelfde figuur maar dan met Finland erbij. Ik geef ook nog Denemarken en Zweden. De landen die Van de Cloot gebruikt zijn in het blauw (behalve België: in het rood). Zweden en Denemarken zijn in het zwart. Finland is ook blauw met een zwarte rand om dat dit land eens wel en eens niet voorkomt in de twee figuren van Van de Cloot.

Dat geeft volgende resultaat voor de nominale cijfers: België staat nu niet op de eerste plaats maar op de tweede, na Finland.

Zoals in de twee eerdere blogposts vermeld, is het gebruik van nominale cijfers om de stijging van overheidsuitgaven te vergelijken tussen landen misleidend. Je moet ook corrigeren voor inflatie en economische groei.

In de tweede figuur corrigeert Van de Cloot voor inflatie. Hij gebruikt echter de HICP: de geharmoniseerde index van consumenten prijzen. Dat is een prijsindex voor de gehele EU die de ECB gebruikt. Het is dus geen inflatie-index per land. Terwijl je dat net nodig hebt: je wil de reële overheidsuitgaven van verschillende landen vergelijken en dus moet je ook de reële uitgaven, zonder het effect van de prijsstijging, van die landen vergelijken. In sommige landen is de prijsstijging hoger dan in andere landen en dus moet je ook voor elk land de prijsindex gebruiken van dat land (je kan kritiek hebben op het feit dat sommige landen een hogere inflatie hebben, maar dat is een andere discussie). Ameco, de databank van de Europese commissie geeft dan ook reële cijfers met een prijsindex per land, de GDP deflator. Dat geeft onderstaande figuur. In de figuur van Van de Cloot met de HICP stond België op de eerste plaats, nu op de tweede plaats.

[UPDATE: Van de Cloot zegt wél de HICP per land te gebruiken. De verschillen tussen de twee figuren zijn dan te verklaren doordat ik de GDP deflator gebruik in plaats van de HICP. De databank van de Europese Commissie (Ameco gebruikt de GDP deflator om te corrigeren voor inflatie – zie rubriek 16.2]

Je moet echter volgens mij de overheidsuitgaven nog eens corrigeren voor de economische groei door de overheidsuitgaven te beschouwen als aandeel van het BBp. Ivan Van de Cloot is het er in ieder geval mee eens dat het de moeite waard is om naar dit cijfer te kijken. Hij geeft echter geen figuur in zijn blogpost en in de pdf waarnaar gelinkt wordt vind ik slechts één figuur met overheidsuitgaven uitgedrukt in procent van BBP, namelijk grafiek 5 en die grafiek geeft enkel van België de evolutie van de primaire overheidsuitgaven van 2000 tot 2012 (over die grafiek of heb ik in het verleden ook al geblogd).

Als je de stijging van de overheidsuitgaven als aandeel van het BBP wil vergelijken, dan kan je de procentuele stijging of de procentpunt stijging geven. Ik denk dat er voor beide manieren iets te zeggen valt en dus geef je ze misschien best alletwee (zoals beschreven in mijn tweede kritische blogpost ivm nominale overheidsuitgaven).

De figuur hieronder geeft de procentuele stijging. België staat nu op plaats zes (plaats 5 als Denemarken en Zweden niet beschouwd worden).

De procentpunt verandering geeft de volgende figuur. België staat nu op plaats vier (plaats 3 als Denemarken en Zweden niet beschouwd worden).

Het mag duidelijk zijn: er is wel degelijk een verschil als je overheidsuitgaven nominaal geeft of uitgedrukt in BBP. Als je overheidsuitgaven wil vergelijken dan doe je dat niet op basis van nominale cijfers. Bovendien is het nog maar de vraag hoe slecht het is dat overheidsuitgaven sterk stijgen tijdens een economische crisis. Over deze twee zaken schreef ik al in de eerste blogpost over dit onderwerp.

Tot slot nog eens wat ik op het einde van die eerste post schreef: “Met deze kritiek op het gebruik van nominale cijfers of op de stijging van de overheidsuitgaven wil ik niet zeggen dat er geen probleem is met overheidsuitgaven in België. Dat kan zeker het geval zijn, maar daar kan je op basis van deze cijfers onvoldoende goed over oordelen, ook niet als ze gecorrigeerd zijn voor inflatie en economische groei: overheidsuitgaven op zich zeggen immers niets.” Polariserend? Ik denk het niet.

Belgische ambtenaren niet zo duur

Posted on January 15, 2013 by Andreas Tirez

Luc Coene van de Nationale Bank heeft van zich laten spreken: het aantal ambtenaren bij de regio’s is ontspoord in de periode 2000-2010. Dat is onhoudbaar als België budgettair op orde wil komen tegen 2015.

Hieronder bekijk ik enkele cijfers van de Oeso wat betreft de ambtenarij (met dank aan Ruben Mooijman voor de getweette link). De cijfers zijn voor 2008. Ik vergelijk daarbij België met zijn buurlanden Duitsland, Nederland, Frankrijk en de UK en met drie Scandinavische landen (Denemarken, Finland en Zweden). Ik neem deze landen omdat ze een buur- en/of topland zijn.

De onderstaande figuur geeft het aantal ambtenaren als aandeel van de totale beroepsbevolking. Hieruit blijkt dat België volgens deze cijfers heel wat minder ambtenaren heeft dan de Scandinavische landen en Frankrijk, wat weinig verrassend is voor mij. Wel verrassend voor mij is dat België ongeveer evenveel ambtenaren heeft als de UK en gevoelig meer dan Nederland en zeker dan Duitsland.

In het federale België is het ook interessant om te kijken naar de verdeling van deze ambtenaren, namelijk het aandeel op centraal (federaal) niveau en op subcentraal (regionaal) niveau. Ook daar heeft de Oeso cijfers voor, te zien op onderstaande figuur (cijfers ontbreken voor Frankrijk en UK; ik heb deze vervangen door Spanje en de VS omdat dit ook federale landen zijn).

Uit deze figuur blijkt dat alle getoonde landen een sterke decentralisatie hebben. De cijfers gelden voor 2008, dus ik vermoed dat de decentralisatie in België na de zesde staashervorming (die momenteel voorbereid wordt) nog sterker zal zijn. Als er gesnoeid moet worden in het aantal ambtenaren, dan zal het grootste effect dan ook bij de regio’s liggen, wat Luc Coene dus ook vraagt.

Ook Caroline Ven en haar co-auteur Niko Gobbin hebben dit in het verleden reeds geschreven in hun boek ‘Welvaartsval’ (waar ik indertijd heel wat van opgestoken heb): het vet is van de soep op federaal niveau. En ook VOKA heeft in het verleden de grote aangroei van ambtenaren bij de regio’s aangeklaagd. Niets nieuws onder de zon dus.

Ten slotte wat betreft de kostprijs van die ambtenaren. Zoals gezegd viel het me op dat Nederland en Duitsland weinig ambtenaren in dienst hebben. Ik verwijs opnieuw naar het boek ‘Welvaartsval’ waairn de auteurs opmerken dat het aantal ambtenaren niet alles zegt en dat met name in Nederland (als ik me goed herinner) het relatief lage aantal ambtenaren gecompenseerd wordt door meer uit te besteden, met navenant hogere kosten voor de aankoop van goederen en diensten. Dat blijkt ook uit de onderstaande figuur (weerom cijfers Oeso).

Nu blijkt Nederland plots het tweede duurste land van het rijtje te zijn en blijkt België helemaal niet zo’n duur ambtenarenapparaat te hebben. Enkel Duitsland is fors goedkoper en blijkt hier het gidsland te zijn.

Het lijkt dus wel mee te vallen met het aantal ambtenaren in België (hoewel er op basis van deze cijfers zeker ruimte voor verbetering is als je België vergelijkt met Duitsland).

Hoe komt het dan toch dat we in België zo veel klagen over de te hoge belastingen? Dat is volgens mij te verklaren doordat arbeid zwaar belast wordt en omdat België heel sterk de inkomensongelijkheid reduceert via herverdeling. Zie hiervoor een vorige blogpost.

economieblog

opinions are cheap, facts are expensive

Tag Archives: meten is weten