In een vorige blogpost besprak ik de financieringskosten van België en de impact eind 2011 van de ‘Leterme-bons’ en de vorming van de regering Di Rupo. Volgens mij deden die twee gebeurtenissen de financieringskosten van de Belgische overheden dalen. Ik steunde me onder meer op een figuur van Peter Vanden Houte, hoofdeconoom bij ING, die hij toonde tijdens een presentatie en de bijbehorende uitleg: volgens hem veranderden die twee genoemde gebeurtenissen hoe de marktspelers de kredietwaardigheid van België evalueerden: die evolutie was positief waardoor de risicopremie die België moest betalen significant daalde.

Kurt Verstegen, een blogger en professioneel bezig met onderzoek over financiële markten, onderzocht mijn stelling kritisch: op basis van een statistische analyse zag hij geen factoren die specifiek voor België de financieringskost significant verlaagden. Hij schrijft in zijn conclusie onder meer dit:

Al bij al zijn de feiten dat één factor het grootste deel van de spreads drijft. En dat de claim dat de daling van onze financieringskosten vooral het resultaat is van goed werk van de regeringen daarmee een beetje in het water valt.

Data-analyse op een hoger niveau

Kurt gebruikt voor zijn analyse de techniek van principale componenten analyse. Het is een techniek die tracht de achterhalen of en in welke mate er een gemeenschappelijke factor is die de waargenomen variatie van verschillende variabelen kan verklaren. De verschillende variabelen zijn in deze oefening de rente die de verschillende landen moeten betalen op zijn schuld (of de spread met Duitsland).

De techniek is zowat het eerste wat je te leren krijgt bij multivariate statistiek, maar het is – althans wat mij betreft- data-analyse op een hoger niveau. Het gaat niet meer over het maken van een aantal grafieken of het berekenen van een aantal correlaties.

Ik ben van mening dat het geven en analyseren van cijfers het begin is van een maatschappelijke discussie, niet het einde ervan. En zij die deelnemen aan de discussie moeten bereid zijn cijfers proberen te interpreteren, ook al is dat niet altijd even gemakkelijk. Als de probleemstelling en de discussie geholpen worden door moeilijke(re) statistische technieken te gebruiken, dan moet dat gebeuren, ook al kost dat (heel) wat moeite.

Anderzijds is het zo dat ook moeilijkere statistische technieken niet noodzakelijk het correcte antwoord geven. En ook kritiek op deze methode kan nodig zijn. Hieronder ga ik de methode en de resultaten van de principale componenten analyse van Kurt behandelen.

Ik analyseer de rente, niet de spread met Duitsland. Ik weet niet of dat veel verschil maakt, maar Finland en Nederland lijken eveneens sterke risk free waarde te hebben (Frankrijk en Oostenrijk minder), waardoor de spreads in absolute waarde zeer weinig fluctueren, waardoor ik me afvraag of ze de resultaten niet vertekenen (maar dat weet ik dus niet).

1. 90% gemeenschappelijkheid kan veel verhullen

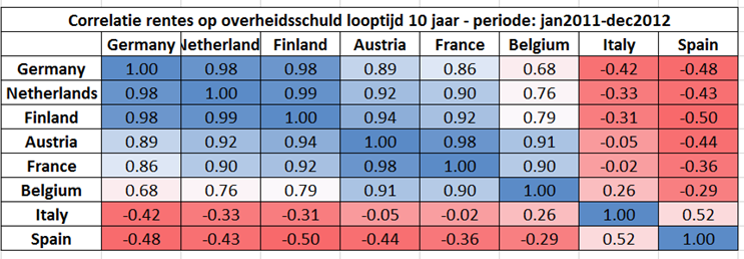
De techniek van de principale componenten analyse gebruikt als input de covariantiematrix van de variabelen. Hieronder toon ik de correlatiematrix van deze variabelen (correlaties zijn covarianties die genormaliseerd zijn door de standaarddeviaties met als resultaat een waarde tussen -1 en 1).

Als de gemeenschappelijkheid van België met de kernlanden wordt geanalyseerd, dan blijkt deze volgens Kurts analyse 90% te zijn. Heel veel variatie van België én de kernlanden wordt dus verklaard door één factor, en dat kan dus niet de regeringsvorming zijn of de Leterme-bons omdat dat specifiek voor België een impact zou gehad hebben en niet op de andere landen (men kan ook dat betwijfelen, maar laten we dat nu aannemen). De periode die Kurt analyseert is 2011 en 2012.

Echter, zoals te zien is op correlatiematrix, zijn de kernlanden sterker met elkaar gecorreleerd dan België. Misschien verklaart de gemeenschappelijke factor wel heel veel variatie van de kernlanden, maar minder van België, en veel minder van Spanje en Italië.

Dat wordt volgens mij ook bevestigd als je de factor loadings bekijkt van de eerste factor. Kurt heeft deze in een bijkomende analyse gepubliceerd (zie pagina 3 van dit document). Daaruit blijkt dat de “factor loadings” op de eerste component hoog zijn voor de kernlanden: tussen 0,402 (voor Frankrijk) en 0,557 (voor Finland). Voor België is deze 0,301, voor Italië 0,204.

Ik weet niet zeker of mijn kritiek op de principale componenten analyse klopt, maar bekijk het eens zo: stel dat er vijf landen zijn die exact hetzelfde patroon vertonen: bij deze landen zal een principale componenten analyse alle variatie verklaren door één factor. Als je er dan één land bijvoegt dat een ander patroon volgt dan die vijf landen, dan zal de principale componenten analyse nog steeds concluderen dat één factor veel variatie verklaart. En als dat bijgevoegde land in een bepaald periode niet hetzelfde patroon volgt en tijdens een andere periode wél, dan zal de verklaringskracht van die ene factor nog stijgen.

2. Voor en na BeGov

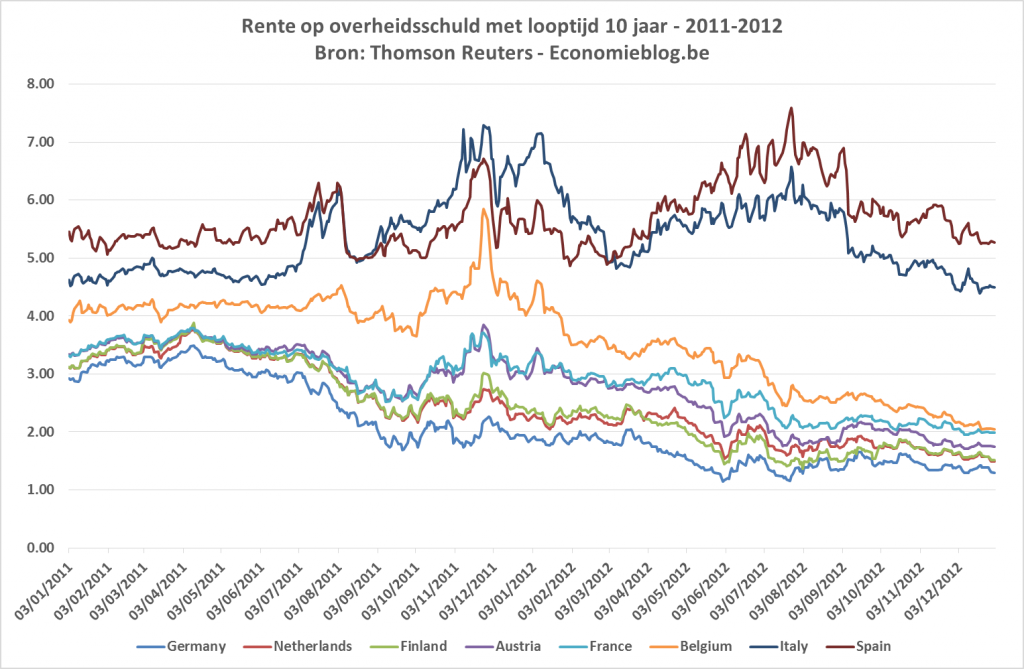
De principale componenten analyse wordt dus toegepast op de hele tijdsreeks, waarmee ik bedoel zowel voor als na de regeringsvorming. Het punt is echter dat er volgens mij een breuk in de tijd is: de figuur met de rentes (of de risicopremie), die ik hieronder herneem voor de beschouwde periode, lijkt te suggereren dat België vóór de regeringsvorming eerder bij de perifere landen zoals Italië en Spanje gerekend werd, terwijl België na de regeringsvorming (zeker na verloop van tijd) naar de kernlanden opschuift.

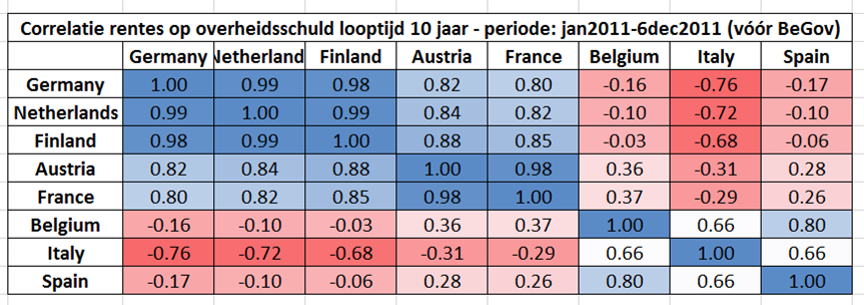
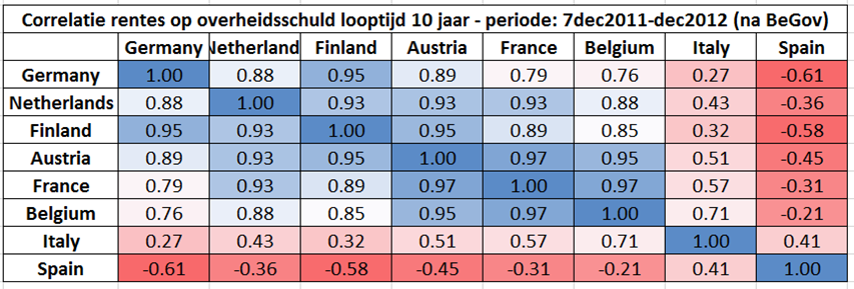
Hieronder geef ik dezelfde correlatiematrix als hierboven, maar dan één voor de periode vóór de regeringsvorming (van 1 januari 2011 tot 6 december 2011) en één na de regeringsvorming (van 7 december 2011 tot 31 december 2012).

Vóór de regeringsvorming is de correlatie van België met de kernlanden laag, soms zelfs licht negatief. Italië en Spanje hebben lage positieve tot grote negatieve correlaties met de kernladen. Duitsland, Nederland en Finland lijken echt de kern te vormen; Oostenerijk en Frankrijk zitten er kort tegen, maar vormen toch een groepje apart.

Na de regeringsvorming verandert dit beeld compleet: België komt nu in het groepje van Oostenrijk en Frankrijk dat zelf meer tot de kernlanden lijkt te gaan behoren.

Ook de correlatie van Italië met de kernlanden Duitsland, Finland en Nederland verandert sterk: van sterk negatief (rond -0,7) naar gematigd positief (rond +0,35).

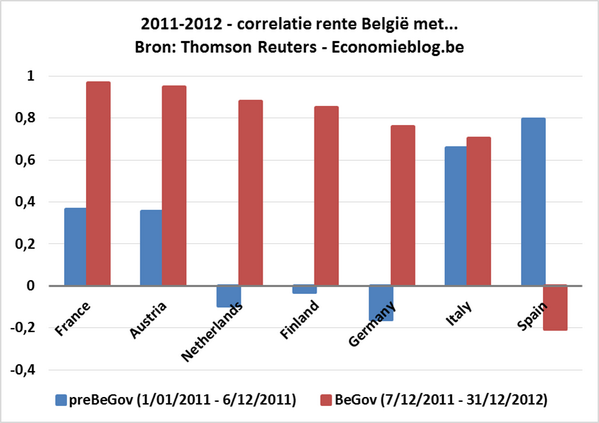
De onderstaande figuur vat de cijfers uit de twee bovenstaande correlatiematrices samen voor wat betreft België. De correlatie van België met de kernlanden vóór de regeringsvorming wordt gegeven door de blauwe balkjes: correlatie is laag tot zelfs negatief. Na de regeringsvorming (rode balkjes) is deze zeer hoog: de verandering is spectaculair te noemen.

Omgekeerd verandert de correlatie met Spanje sterk: vóór de regeringsvorming is deze hoog, erna wordt deze negatief. Enkel de correlatie van België met Italië is het op eerste gezicht vreemd: deze blijft min of meer gelijk.

3. Italië en België: een gelijkaardige politieke evolutie?

Het patroon van Italië is speciaal: voor en na de Belgische regeringsvorming blijkt ook het patroon van de Italiaanse rente sterk te veranderen, namelijk eerst een sterk negatieve correlatie met de kernlanden, die na de Belgische regeringsvorming gematigd positief is. Di Rupo mag dan al Italiaanse roots hebben, maar een dergelijke impact kunnen we niet toeschrijven aan de Belgische regeringsvorming.

[Hoewel ook dat kan betwijfeld worden: de financiële wereld is sterk verbonden met elkaar. Dat heeft het bankroet Lehman Brothers, dat de hele financiële wereld op haar grondvesten deed daveren, duidelijk aangetoond. En ook een eventueel ongecontroleerd Grieks bankroet deed de hele eurozone beven. Het is dan ook niet onzinnig om te veronderstellen dat een verhoogd risico op een Belgische wanbetaling ook andere (Europese) landen in problemen kan brengen, met verhoogde rentes tot gevolg.]

Er is in die periode echter ook iets belangrijk gebeurd in de Italiaanse politiek: Berlusconi nam ontslag als premier op 12 november 2011 en werd een paar dagen later vervangen door Mario Monti, iemand die uit de financiële wereld komt en het vertrouwen genoot van de spelers op deze markt. Met andere woorden, het gevaar op politieke instabiliteit in Italië verminderde wellicht sterk in november 2011 en de tijd erna.

Conclusie

Volgens mij moet er dus een analyse gemaakt worden voor en na de federale regeringsvorming. Als Kurt met een dergelijke analyse komt die statistisch aantoont dat er geen significant verschil is tussen voor en na de regeringsvorming, of dat het verschil wel significant is maar dat de impact klein is, dan zal ik dat kritisch bekijken. Als ik geen argumenten vind om dat te ontkrachten, dan zal ik mijn stelling daaraan aanpassen.

Tevens denk ik dat het patroon van Italië eerder de stelling versterkt dat politieke (in)stabiliteit een impact heeft (of tenminste had) op de rente die een overheid op de schuld moet betalen.

En een meta-conclusie: dit is het soort debat dat ik graag meer wil voeren: over cijfers en de analyse ervan. Dat kan je natuurlijk niet alleen, maar Twitter en blogs lenen zich perfect voor dit soort discussies. En bij deze dus een volgtip voor Kurt Verstegen.