» De vreemde dynamiek van de overheidsschuld

De overheidsschuld staat vaak centraal in discussies over het beleid van de overheid. Dat zal met de komende begrotingsbesprekingen niet anders zijn. Een goed begrip van de overheidsschuld is dan ook belangrijk en dat is sinds de financiële crisis en de vergrijzing alleen maar toegenomen.

De evolutie en het niveau van de overheidsschuld wordt vaak aangegrepen om de gezondheid en draagkracht van de overheidsfinanciën te illustreren. Een te hoge overheidsschuld kan leiden tot een ineenstorting van de welvaartstaat. Een stijgende overheidsschuld wordt dan ook vaak negatief bekeken.

De Europese Commissie heeft sinds de eurocrisis heel wat bevoegdheden gekregen om de landen van de eurozone te bestraffen indien ze een te groot overheidstekort hebben: landen mogen in principe geen hoger begrotingstekort hebben dan 3% en dat zal in de toekomst nog aangescherpt worden. Dat moet de overheidsschuld in de eurozone stabiliseren.

In een eerdere blogpost heb ik al de impact van de inflatie op de overheidsschuld bekeken. In deze blogpost zal ik een vreemde eigenschap van de overheidsschuld illustreren, namelijk dat een zelfde begrotingstekort kan leiden tot zowel een stijging als tot een daling van de overheidsschuld, afhankelijk van de startpositie.

Om dit te illustreren simuleer ik de 20-jarige evolutie van de overheidsschuld van twee fictieve landen die schijnbaar gelijke prestaties afleggen, echter enkel verschillen wat betreft de initiële overheidsschuld (of beter: schuldratio).

Beide landen hebben gedurende 20 jaar:

een reële groei van 2% per jaar
een inflatie van 2% per jaar
een begrotingssaldo van -2% jaar (een begrotingstekort)
een jaarlijkse interest van 4% per jaar op hun uitstaande overheidsschuld

Het eerste land heeft een initiële schuldratio van 100%; het tweede land een initiële schuldratio van 20%.

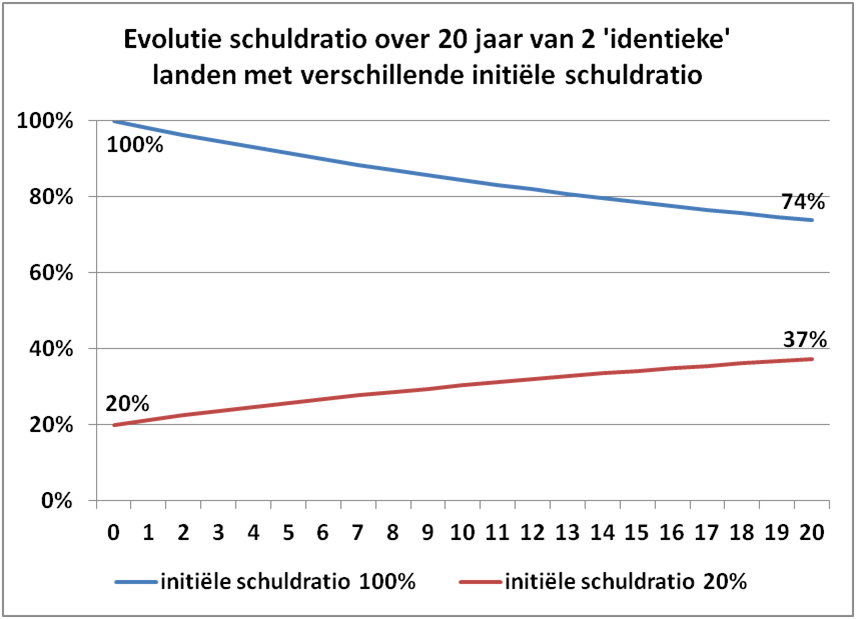
De onderstaande figuur geeft de evolutie van de schuldratio van de twee landen voor de komende 20 jaar . En deze evolutie is opmerkelijk: beide lande presteren economisch op het eerste gezicht perfect gelijk, maar de schuldratio daalt in het land met hoge schulden van 100% naar 74% en stijgt in het land met lage schulden van 20% naar 37%. Formeel kan aangetoond worden dat de schuldratio voor beide landen asymptotisch zal evolueren naar 52% (zie onderaan deze blogpost voor een formele afleiding).

Bron: eigen simulatie (xls)

Het land met hoge schulden lijkt het dus veel gemakkelijker te hebben om de schuldratio af te bouwen dan het land met lage schulden. Dat lijkt niet logisch.

En dat is ook niet het geval. Wat hier beschouwd werd was het uiteindelijke begrotingstekort, dat 2% verondersteld werd. Het begrotingstekort is inclusief de interest die het land moet betalen op zijn uitstaande overheidsschuld. Met de veronderstelling dat de interest op de schuld 4% per jaar is, moet het land met een initiële schuldratio van 100% het eerste jaar 4% van het BBP gebruiken om de interest te betalen; het land met 20% overheidschuld moet maar 0.8% van het BBP aan intrest betalen. De betalingen van interest op overheidsschuld is een last uit het verleden dat niet onmiddellijk iets te maken heeft met de prestaties in het huidige jaar.

Om de prestaties te kunnen beoordelen voor het huidige jaar, moet er gekeken worden naar het begrotingstekort exclusief de interestbetalingen, het zogenaamde primair saldo (of primary surplus). Het primair saldo is in het eerste jaar +2% voor het land met hoge schulden en -1,2% voor het land met lage schulden. Het land met hoge schulden doet het dus eigenlijk een pak beter dan het land met lage schulden, alleen is dit niet te zien in het begrotingstekort, maar enkel in het primair saldo. En dat betere primair saldo is de verklaring dat de schuldratio daalt voor het land met hoge schulden en stijgt voor het land met lage schulden (evenals het effect van de nominale groei).

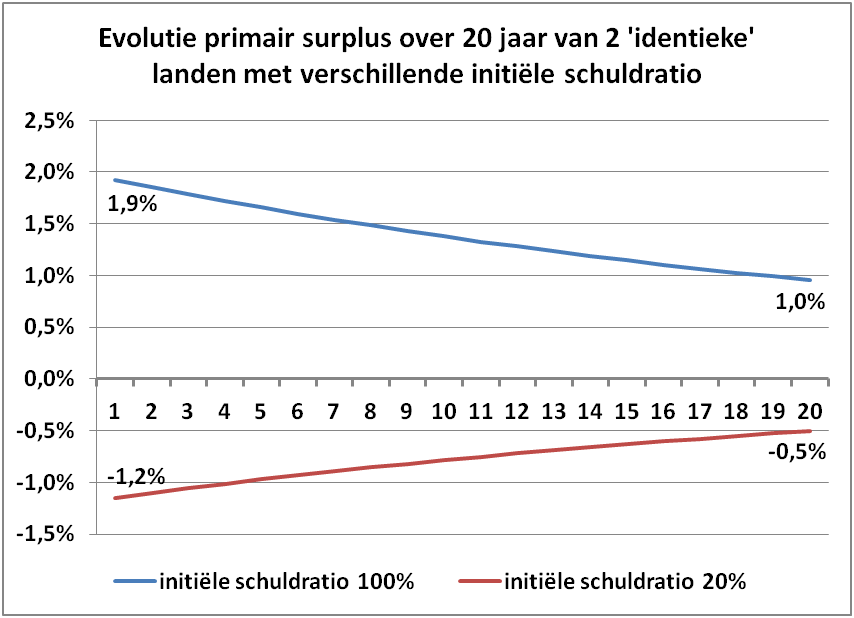
Naarmate de jaren verstrijken en gezien in deze simulatie het begrotingssaldo constant wordt gehouden op -2%, zal het primair saldo afnemen voor het land met hoge schulden, maar het blijft in deze simulatie positief. Voor het land met lage schulden verbetert het primair saldo maar blijft het negatief, zoals te zien op de onderstaande figuur.

Bron: eigen simulatie (xls)

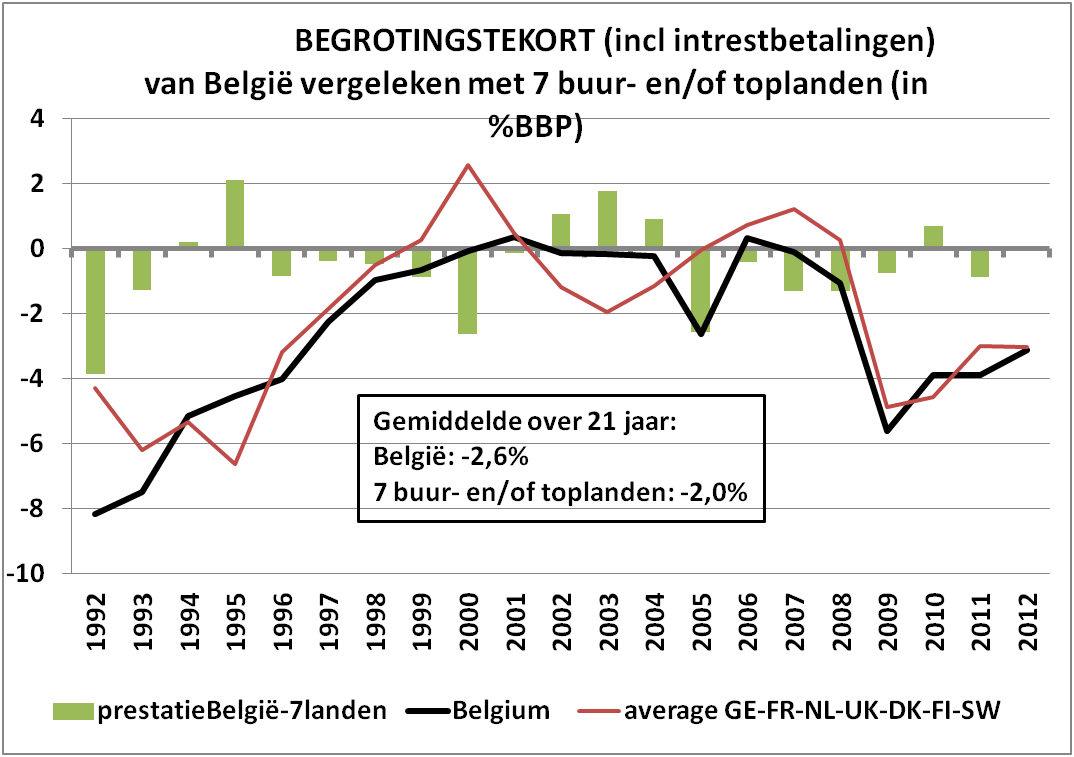
Het bovenstaande is theorie, maar kan ook in de praktijk waargenomen worden. Hieronder de grafiek met de evolutie van de laatste 21 jaar van het begrotingstekort van België en het gemiddelde begrotingsterkort van zeven buur- en/of toplanden (zijnde Nederland, Frankrijk, Duitsland, UK, Denemarken, Finland en Zweden). België wordt voorgesteld door de zwarte lijn, het gemiddelde van de 7 landen door de rode lijn. De groene balkjes op de figuur geeft het verschil tussen België en het gemiddelde van de 7 landen. Hieruit blijkt dat het begrotingstekort van België gemiddeld -2,6% was; dat van de 7 buur- en/of toplanden was gemiddeld -2%; België presteert dus iets slechter dan het gemiddelde van de 7 landen.

Bron: Ameco

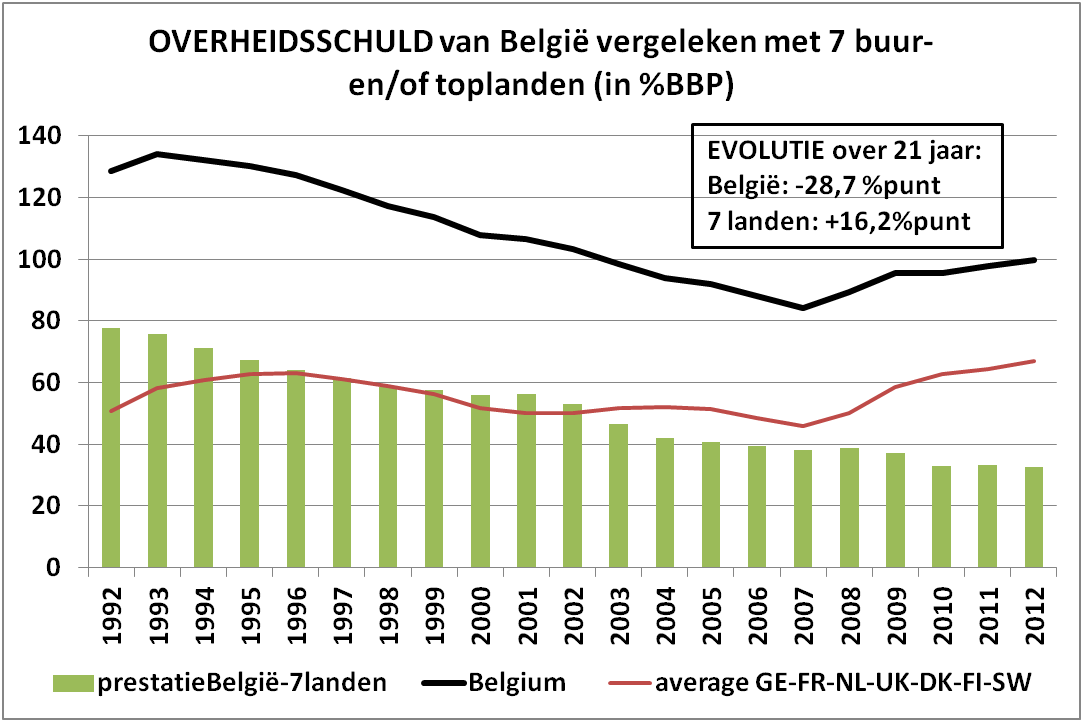
Echter, als er gekeken wordt naar de evolutie van de schuldratio over dezelfde periode voor dezelfde landen, dan blijkt de schuldratio van België steeds veel hoger te zijn dan het gemiddelde van de 7 landen, maar de Belgische schuldratio is wel fors afgenomen (met bijna 29 procentpunt) terwijl die van de 7 landen gemiddeld is toegenomen (met 16 procentpunt): België presteerde de laatste 21 jaar dus 45 procentpunt beter wat betreft de vermindering van de schuldratio, ondanks een slechtere prestatie wat betreft het begrotingstekort.

Bron: Ameco

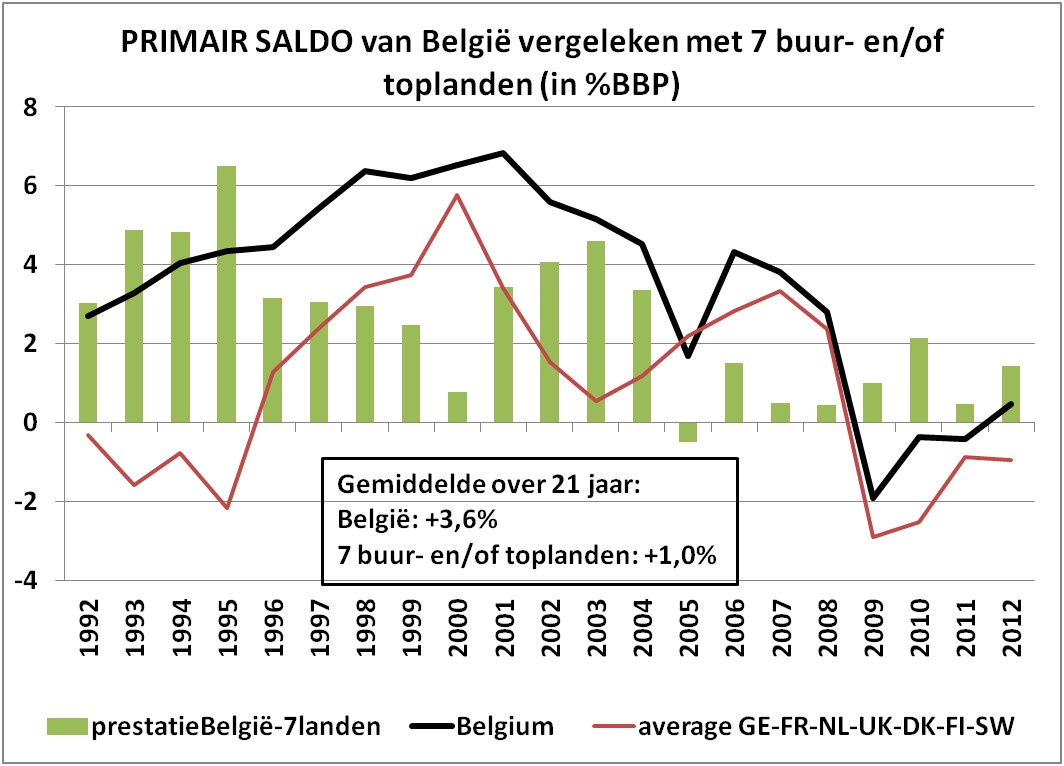
Dat is echter niet zo vreemd, zoals hierboven geïllustreerd door de simulatie, als er gekeken wordt naar de evolutie van het primair saldo, het begrotingssaldo zonder intrestbetalingen op de overheidsschuld. De onderstaande grafiek geeft deze evolutie voor dezelfde landen en dezelfde periode. Het gemiddelde primair saldo voor België is +3,6%; dat van de 7 landen slechts +1%.

[noot in de marge: de groene balkjes geven het verschil van het Belgisch primair saldo met het gemiddelde primair saldo van de 7 buur- en/of toplanden; dat 7-landen-gemiddelde dient als benchmark. Twee opmerkelijke zaken: (1) België heeft gedurende 20 van de 21 jaar een primair saldo dat hoger ligt dan het gemiddelde van de 7 buur- en/of toplanden; (2) tijdens de periode 2001-2004 (grosso modo Verhofstadt I) kent België een hoger primair saldo in vergelijking met de 7 buur- en/of toplanden dan de periode 1996-1999 (grosso modo Dehaene II)]

Bron: Ameco

Op basis van het bovenstaande is het begrotingstekort niet de goede maatstaf om prestaties van landen te willen beoordelen. Daarvoor zou men beter kijken naar het primair saldo of, nog beter, gewoon naar het niveau en de evolutie van de schuldratio.

Als we de schuldratio beschouwen, dan blijkt België de laatste 21 jaar een topprestatie te hebben afgeleverd, indien België vergeleken wordt met het gemiddelde van de genoemde buur- en/of toplanden.

———————————

Formele afleiding – de vreemde dynamiek van de schuldratio

Totale economische activiteit : GDP in euro
Totale overheidsschuld: D in euro
Schuldratio: schuld in % van GDP: SR = D/GDP (in % van GDP)

Jaarlijkse reële groei (in % per jaar): r
Jaarlijkse inflatievoet (in % per jaar): i
Jaarlijkse begrotingstekort (in % van GDP): d

Referentiejaar 0

Stel op referentiejaar 0 is
Totale economische activiteit = GDP0
Totale overheidsschuld (D) in euro = D0
=> schuldratio (SR) in referentiejaar 0 = SR0 = D0 / GDP0

Jaar 1

GDP1 = GDP0 + (i+r) * GDP0 = (1+i+r) * GDP0
D1 = D0 + d * GDP1

Jaar 2

GDP2 = (1+i+r) * GDP1 = (1+i+r) * (1+i+r) * GDP0 = (1+i+r)2 * GDP0
D2 = D1 + d * GDP2 = D0 + d * GDP1 + d * GDP2 = D0 + d * [GDP1 + GDP2]

Jaar n

GDPn = (1+i+r)n * GDP0
Dn = D0 + d * [GDP1 + GDP2 + … + GDPn] = D0 + d * Σ GDPj met j = 1 tot n

=> Dn = D0 + d * GDP0* Σ (1+i+r)j met j = 1 tot n

Gegeven dat: