Deze post gaat over de verdeling van de economische productie tussen arbeid (L van Labour) en kapitaal (K). Het is een discussie die in de toekomst waarschijnlijk belangrijker wordt, omdat de robots het zullen overnemen.
Een recente Twitter-conversatie ging over wat er gebeurt als een boer een tractor koopt. Daardoor verhoogt het kapitaal waarover de boer beschikt. Dan kan het loonaandeel van die boer alleen maar dalen, zo stelde Koenfucius. Als de boer nog geen machines had voordat hij een tractor kocht, dan klopt dit. Maar dit is een extreem verhaal en niet nuttig om te begrijpen wat er met de totale economie zou gebeuren als er meer in kapitaal wordt geïnvesteerd.
Nuttiger is om te veronderstellen dat de boer wel al machines heeft en een tractor bijkoopt. Met die extra tractor kan hij dan meer produceren dan het jaar ervoor.
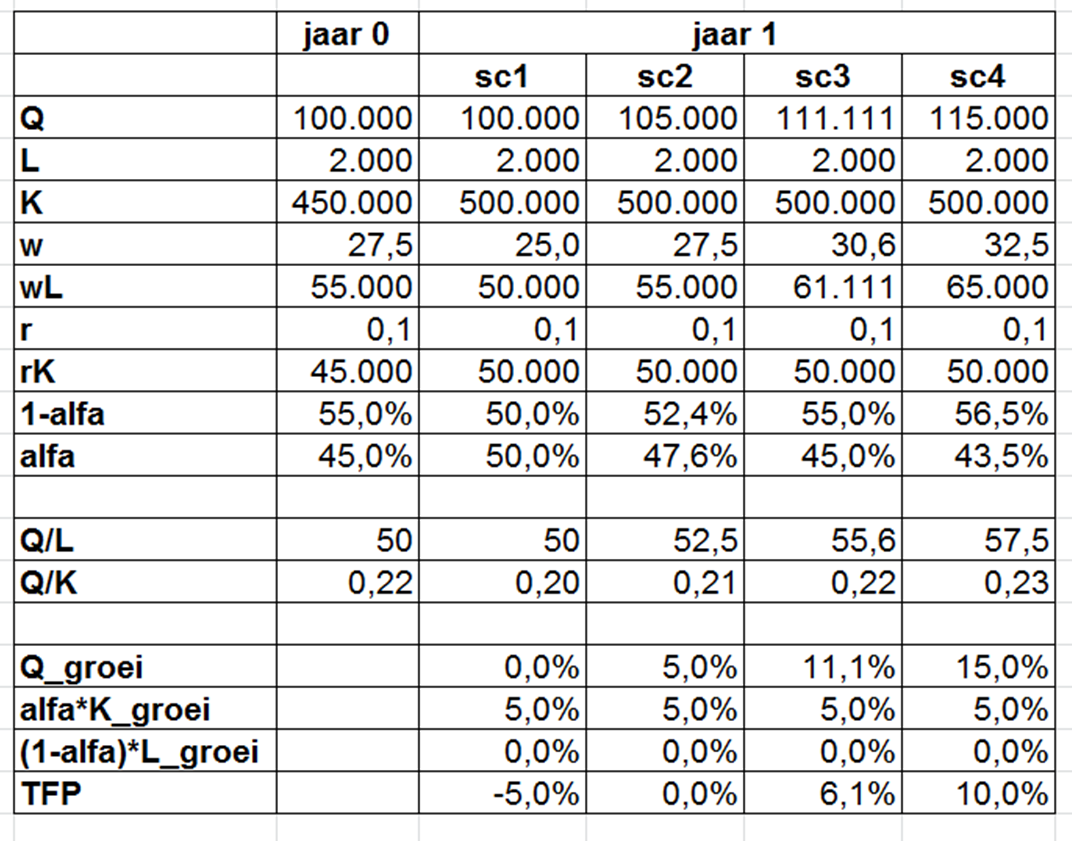
Hieronder een tabel met een fictieve situatie: in jaar 0 heeft de boer voor 450.000 kapitaal (K) tot zijn beschikking waarop hij jaarlijks 10% rente (r) betaalt aan de bank. Deze rente is vast en moet betaald worden (anders gaat hij bankroet). De boer werkt 2000 uren (L) en heeft een bruto-winst van 100.000 (Q). Daarvan gaat dus 45.000 (rK) naar de bank en krijgt de boer 55.000 (wL) of 27.5 per uur (w). Het loonaandeel (1-alfa) in de winst is dus 55%.
In jaar 1 koopt de boer een extra tractor van 50.000 en werkt hij evenveel uren als in jaar 0. Ik veronderstel vier scenario’s, afhankelijk van de productie.
- Scenario 1: er is nulgroei: ondanks de extra tractor maakt de boer geen extra winst. Toch moet hij nu 50.000 aan de bank betalen, wat betekent dat er slechts 50.000 overblijft voor de boer, wat overeenkomt met 25 per uur. Het loonaandeel is gedaald van 55% naar 50%.
- Scenario 2: door de extra tractor is de winst gestegen tot 105.000. Opnieuw krijgt de bank 50.000 en blijft er 55.000 over voor de boer: zijn loon is dus 27,5 per uur gebleven ten opzichte van jaar 0, maar het loonaandeel is gedaald van 55% tot 52,4%.
- Scenario 3: de winst is nu gestegen tot 111.111. Er blijft dus 61.111 over voor de boer of ruim 30 per uur. Het loon is dus gestegen, maar het loonaandeel is constant op 55%.
- Scenario 4: de winst stijgt in dit scenario met 15% tot 115.000. Nu is niet enkel het loon gestegen, tot 32,5 per uur, maar ook het loonaandeel stijgt van 55% naar 57,5%.
Met andere woorden, alles is mogelijk: het loonaandeel kan dalen, gelijk blijven of stijgen. Het hangt af van hoe nuttig of productief de extra tractor kan ingezet worden.
Dat nut of die productiviteit wordt niet enkel door de technische capaciteit bepaald (namelijk hoeveel hectares de tractor kan bewerken) maar ook door wat de productie uiteindelijk oplevert op de markt. Als de markt voor de boer tegenzit en de prijzen dalen, dan zal de productiviteit dalen, ondanks het feit dat men meer land bewerkt heeft (scenario 1). Als de markt meezit voor de boer en de prijzen stijgen fors, dan is de winstgroei plots veel hoger (scenario 4) en is de tractor economisch veel productiever (hoewel de technische productiviteit niet hoger wordt). Of misschien heeft de boer zich bijgeschoold en kan hij de extra tractor slimmer inzetten waardoor de productie stijgt.
Er zijn dus veel factoren die de productiviteit bepalen: niet alleen technische factoren (technologische innovatie, zoals een betere tractor), maar ook de marktomstandigheden en het intelligenter inzetten van arbeid en kapitaal. En er zijn nog factoren, zoals schaalvoordelen.
Groeiboekhouding
Het bovenstaande voorbeeld is interessant om de theorie van de groeiboekhouding op toe te passen. Deze theorie gebruikt een model om ex-post na te gaan welke componenten van de productiefactoren (arbeid of kapitaal) verantwoordelijk zijn voor de extra groei. Dat model is in essentie een wiskundige vergelijking die aangeeft hoe arbeid en kapitaal in productie wordt omgezet, en een assumptie over de beslissing om meer of minder arbeid en kapitaal te gebruiken. Het model wordt onder meer door de Europese Commissie gebruikt.
Dit model leidt tot het opdelen van de economische groei in drie componenten: de arbeidsgroei (L_groei in de bovenstaande tabel) , de kapitaalgroei (K_groei) en de restcomponent. De bijdrage van de arbeid- en kapitaalsgroei wordt gecorrigeerd voor hun aandeel dat deze factoren hebben, respectievelijk het loonaandeel (1-alfa) en het kapitaalaandeel (alfa); in de tabel geeft dit alfa*K_groei en (1-alfa)*L_groei.
De restcomponent is het deel van de groei dat het model niet kan verklaren. Het wordt vaak aangeduid met TFP wat staat voor totale factorproductiviteit of kortweg de productiviteit. Deze interpretatie die economen geven aan de restcomponent is best wel merkwaardig: alles wat het model niet kan verklaren wordt onder de noemer productiviteit gebracht. Natuurlijk is er technologische innovatie die de productiviteit verhoogt en die niet door L of K geleverd wordt, maar zoals hierboven reeds gezegd zijn er andere factoren die de gemeten productiviteit kunnen verklaren.
In het bovenstaande voorbeeld is het kapitaalaandeel in jaar 0 gelijk aan 45%. Als er in jaar 1 een tractor wordt bijgekocht dan stijgt het kapitaal met 11,11% (van 450.000 naar 500.000). Volgens het bovenstaande model is de bijdrage van kapitaal tot de veranderde output daarmee vastgelegd, namelijk 45% * 11,11% = 5%, en dat is onafhankelijk van wat de productiegroei in jaar 1 uiteindelijk wordt. Valt die productiegroei tegen (uitgedrukt in geldtermen), dan is de restcomponent of TFP-groei negatief (scenario 1). Is die productiegroei net gelijk aan 5% dan is de TFP-groei nul: het model heeft alle groei verklaard in termen van K en L. Is de productiegroei sterk positief (scenario’s 3 en 4) dan is de TFP-groei volgens dit model positief.
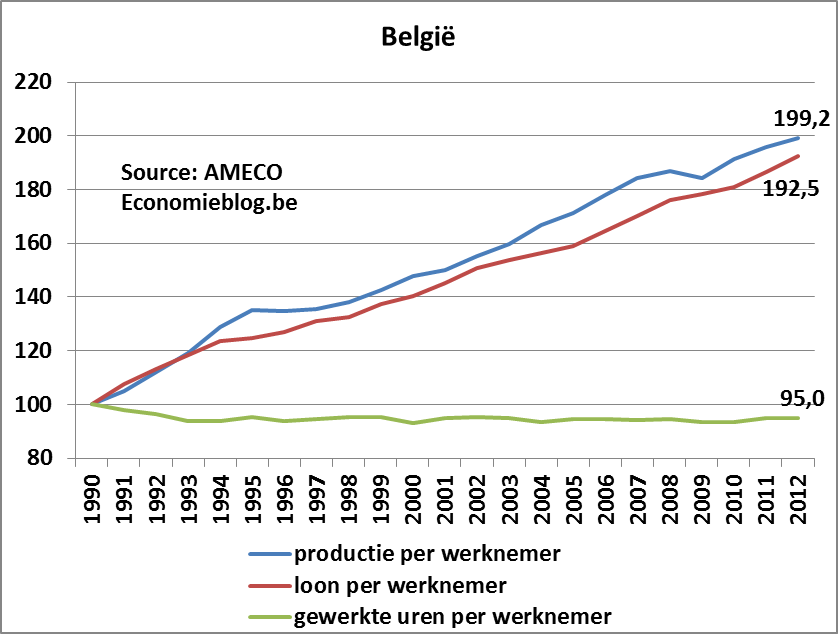
Men kan afleiden dat als het loon de arbeidsproductiviteit volgt, het loonaandeel constant blijft. Of omgekeerd: als het loonaandeel constant blijft, volgt het loon de arbeidsproductiviteit. Dat is wat historisch ook min of meer gebeurd is, zoals te zien is op onderstaande figuur. De figuur geeft de evolutie sinds 1990 van de productie per werknemer en het loon per werknemer. De trend is duidelijk: ze gaan gelijk op. Ten opzichte van 1990 is de productie per werknemer iets meer gestegen tegenover het loon. Maar het aantal gewerkte uren is ook licht gedaald, wat een deel kan verklaren.
In het bovenstaande voorbeeld is geen bijdrage van arbeid tot groei, omdat de boer geen extra uren werkt (hij werkt elk jaar exact 2000 uren). De groei komt dus van de extra tractor. Toch kan men met één extra tractor verschillende uitkomsten hebben (de vier scenario’s).
De TFP-groei wordt volgens mij te weinig kritisch bekeken. Nu wordt het model als gegeven beschouwd en wordt er zoveel mogelijk gestreefd naar TFP-groei (want het is groei die niet moet vergoed worden, zoals dat wel moet bij gebruik van arbeid en kapitaal). Maar dat is de omgekeerde wereld: beter zou zijn om een model proberen te maken dat de economische groei beter kan beschrijven, wat betekent dat de restcomponent (TFP) lager wordt. Men zou dan beter kunnen weten van waar de gestegen of gedaalde productiviteit komt.

koenfucius
June 21, 2013 at 2:43pmIk zie een paar problemen met je verhaal.
1. Je beschouwt winst en loon als uitwisselbaar. Ik denk niet dat dit in het algemeen overeenstemt met de realiteit.
2. Je zondert bankrente af. Ik denk niet dat dit relevant is: misschien gaat het om een rijke boer, die niet hoeft te lenen om een tractor te kopen. De totale opbrengst op het geinvesteerde kapitaal bevat impliciet (opportunity cost) of expliciet (bankrente) de kost van het kapitaal.
3. De marktprijs is eigenlijk ook niet relevant: prijsfluctuaties zouden evenzeer het scenario zonder nieuwe tractor beinvloeden.
Laten we een alternatieve versie maken van je verhaal, waarin deze problemen niet voorkomen: een boer met een boerderij die 450,000 waard is, met een arbeider die al het werk doet. (De boer is dus gewoon een kapitalist.) Het enige verschil tussen jaar 0 en jaar 1 is de aanschaf van de tractor: we willen nl. het effect bekijken op het verhogen van kapitaal om de productiviteit te verhogen. Al de rest blijft netjes ongewijzigd.
In jaar 0 produceert de boerderij 100,000.
De arbeider verdient 12/u en werkt 2000 uren per jaar. Zijn loonkost is 24,000.
De brutowinst voor de boer is dus 76,000, wat het kapitaalsaandeel 76% maakt, en het arbeidsaandeel dus 24%.
In jaar 1 koopt hij een nieuwe tractor (de oude houdt hij in reserve), en verhoogt dus het kapitaal met 50,000.
Dit maakt de werkman meer productief.
10% productiever = 10,000 extra brutowinst voor de boer: 86,000 = 78.2% (==> arbeid = 21.8%)
20% productiever = 20,000 extra brutowinst voor de boer: 96,000 = 80% (==> arbeid = 20%)
Het is natuurlijk mogelijk dat de arbeider een loonsverhoging bekomt, maar dat is een andere kwestie. In afwezigheid hiervan is er principieel geen enkele reden waarom de boer zijn arbeider meer zou betalen: hij werkt net zoveel uren als tevoren (maar met een nieuwere tractor!). Als het wel tot onderhandelen komt is de eventuele daaruit voortkomende verschuiving in arbeid/kapitaal geen mathematisch gegeven, maar bepaald door de relatieve onderhandelingspositie van boer en arbeider.
Als de boer zich concentreert op het rendement op zijn kapitaal, dan is zijn norm de RoC in jaar 0, nl. 76,000/450,000 of 16.89%. De minimum verhoging in de brutowinst om de extra investering van 50,000 te rechtvaardigen is 8,444, dus de minimale productiviteitsverhoging is 8.44%.
Ik denk dat het fundamentele punt is dat zowel het rendement op arbeid als het rendement op kapitaal een subjectief gegeven is. Er is geen natuurwet die bepaalt dat 12 een correct uurloon is, of dat 16.89% een goed rendement op kapitaal is. Maar investeringen gebeuren bijna altijd om het rendement op kapitaal te verhogen (dank zij een productiviteitstoename), en dus is de boer die een nieuwe tractor koopt in de eerste plaats begaan met het effect daarvan op zijn inkomen op het geinvesteerde kapitaal. De productiviteitstoename is uitsluitend toe te schrijven aan de meer efficiente tractor. (In een alternatief scenario kon hij ook een meer efficiente werknemer aantrekken, die hij dan ook meer zou betalen – maar dit is hier niet het geval: de arbeider doet exact hetzelfde in jaar 1 als in jaar 0).
Even een parallel gedachtenexperiment. Stel dat je een schoonmaakster (m/v) hebt die elke week gedurende 3 uur je huis schoonmaakt. In die tijd kunnen alle kamers behalve een worden gestofzuigd – je hebt namelijk een oude bak van een stofzuiger. Je besluit een nieuwe, meer efficiente stofzuiger te kopen, en nu kan de schoonmaakster (m/v) wel alle kamers stofzuigen. Ga je een hoger uurloon betalen omdat je een nieuwe stofzuiger hebt gekocht die de schoonmaakster (m/v) meer productief maakt?
Het lijkt me niet correct in dit geval TFP in te roepen. TFP helpt zeker wanneer er een productiviteitstoename is die noch aan arbeid noch aan kapitaal kan worden toegeschreven – bv. wanneer operationele processen worden verbeterd zonder investeringen. Bij onze boer is de productiviteitsstijging helemaal het gevolg van de aankoop van de nieuwe tractor. Zoals je zelf zegt: “In het bovenstaande voorbeeld is geen bijdrage van arbeid tot groei, omdat de boer geen extra uren werkt” – in mijn voorbeeld is het de arbeider, maar passons. 🙂
Ik vraag me af of we het eigenlijk niet eens zijn met elkaar: het arbeidsaandeel stijgt niet in absolute termen, het kapitaalsaandeel stijgt wel, dus kan het arbeidsaandeel relatief alleen maar slinken.
Wat het gebruik van TFP betreft: als productiviteit toeneemt dank zij iets anders dan efficientere arbeid of efficientere kapitaalsgoederen, dan kun je dat nergens anders onderbrengen dan in dat hokje, denk ik. Een beter model kan daar misschien wat diverse namen aan geven, maar de restcomponent zal niet echt lager worden. In het beste geval kunnen we hem beter benoemen (bv. procesverbetering).