De laatste dagen lijkt het economisch en politiek nieuws alleen maar rond de indexsprong te draaien. Vakbonden en  socialisten zijn tegen, werkgevers en liberalen zijn voor. Hieronder wil ik dit debat vanuit een andere hoek bekijken, namelijk vanuit de staatsschuld en de impact van inflatie op de staatsschuld. Inflatie is de rechtstreekse oorzaak voor een indexaanpassing of -sprong, maar inflatie heeft ook een sterke impact op de staatsschuld.

De staatsschuld wordt immers uitgedrukt ten opzichte van de totale economie, in % van het BBP. Als de economie groeit en de schuld blijft constant (of groeit trager aan dan de economie) dan daalt de schuldratio. En het is de schuldratio die telt, aangezien het een maat is voor de capaciteit van terugbetalen: een overheid kan 100 miljard schuld gemakkelijker terugbetalen indien ze belasting kan heffen op een economie van 1.000 miljard dan indien de economie van het land maar 100 miljard is.

Het BBP wordt op twee manieren gemeten: reëel en nominaal. Een reële groei betekent effectief een groter geldvolume aan goederen en diensten die geproduceerd worden. Nominale groei is gelijk aan de reële groei + de inflatie (of deflatie). Een voorbeeld: stel dat het BBP in jaar 1 gelijk is aan 100. In het volgende jaar is er een reële groei van 2%, en is de inflatie 3%. Het nominale BBP is in dat jaar dan gestegen met 5% tot 105, maar het reële BBP is slechts 102, gerekend in prijzen van jaar 1.

Stel dat de overheidsschuld in het eerste jaar gelijk was aan 80. In dat jaar was de schuldratio 80% (= 80/100). Stel dat de schuld in het volgende jaar stijgt tot 83, dan is de schuldratio in dat jaar gelijk aan 79% (=83/105). Dus ondanks een stijging van de schuld in absolute waarde, daalt de schuldratio. Stel echter dat er geen inflatie was in het tweede jaar, dan was het BBP slechts 102 geweest en dan zou de schuldratio wel gestegen zijn, namelijk tot 81,4% (=83/102).

Inflatie kan dus een belangrijke rol spelen om de overheidsschuld betaalbaar te houden. In feite is inflatie een transfer van mensen (en organisaties) met geld naar mensen (en organisaties) met schuld. Hoe hoger de inflatie, hoe hoger de transfers. En aangezien de overheid veel schulden heeft, kan inflatie helpen om de schulden betaalbaar te houden. En ook belangrijk: hoe hoger de schuld, hoe sterker inflatie de schuldratio kan verminderen (zie ook infra).

Overheden met hoge schulden hebben dus twee redenen om veel inflatie toe te laten: de houdbaarheid van de staatsfinanciën staat onder druk én de gunstige impact van inflatie op de schuldratio is hoog. België, met een schuldratio van 100%, heeft dus een objectief belang bij hoge inflatie.

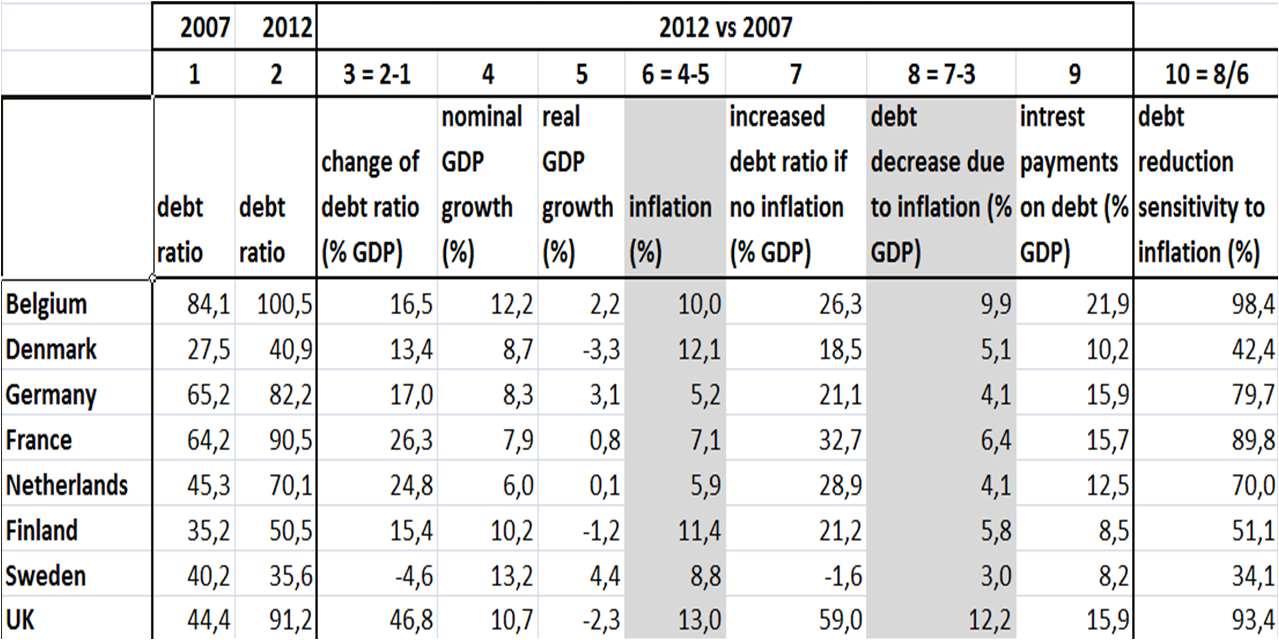
De tabel hieronder geeft aan in welke mate inflatie de Europese overheden tijdens de crisisperiode 2007-2012 geholpen heeft om de schulden te beheersen. Ik bekijk België en zijn buurlanden en drie Scandinavische landen. De kolommen zijn genummerd van 1 tot 10.

Bron: AMECO  –  zie excel-file met de tabel (eigen berekeningen)

In kolom 3 staat de verandering van de schuldratio van 2007 tot 2012. Hieruit blijkt dat België het nog relatief goed gedaan heeft: de schuldratio steeg met 16,5 procentpunt van het BBP, nagenoeg hetzelfde als in Duitsland en veel minder grote stijging dan in Frankrijk en Nederland. Denemarken en Finland deden iets beter en vooral Zweden, met een daling van de schuldratio, is opmerkelijk. Aan de andere kant van het spectrum bevindt zich de UK met een stijging van de schuldratio met 47 procentpunt van het BBP.

Kolom 6 geeft de inflatie over de beschouwde periode. Ook deze varieert sterk. In België was de inflatie in totaal 10%, lager dan Denemarken, Finland en UK, maar hoger dan Zweden, Frankrijk en zeker Duitsland en Nederland. Deze laatste twee blijven onder de zes procent.

Kolom 7 geeft de stijging van de schuldratio indien er geen inflatie zou geweest zijn. Deze is voor alle landen hoger in vergelijking met de werkelijke situatie met inflatie. De relatieve positie van België verslechtert echter ten opzichte van kolom 3: met een stijging van de schuldratio van 26 procentpunt zit België nu boven Duitsland en komen we aardig in de buurt van Nederland.

Kolom 8 geeft de impact van de inflatie op de schuldratio: zonder inflatie zou de Belgische schuldratio 9,9 procentpunt hoger geweest zijn. Frankrijk 6,4 procentpunt; in Nederland en Duitsland heeft inflatie maar voor 4,1 procentpunt geholpen. Enkel de UK had meer baat bij inflatie dan België.

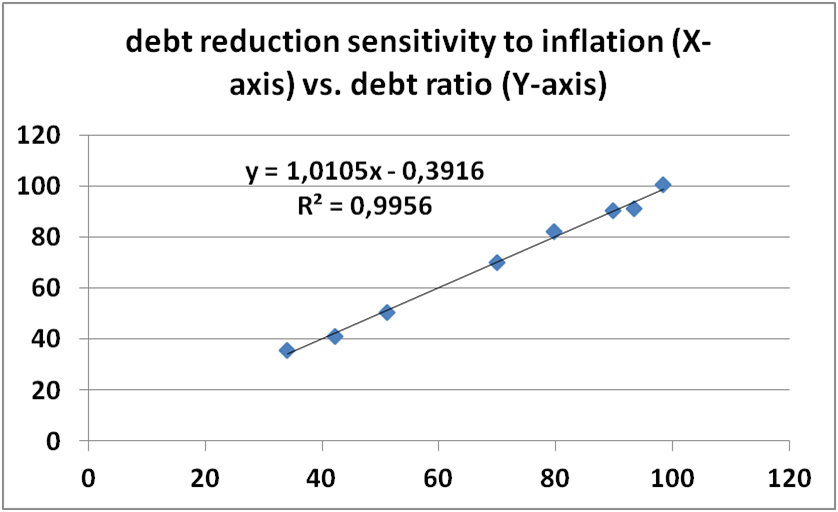
De laatste kolom geeft de gevoeligheid van de schuldratio voor inflatie: voor België is die bijna 100%: als de inflatie stijgt met x %, dan daalt de schuldratio ook met bijna x% (onderaan deze blogtekst wordt deze relatie formeel bekeken). De impact van inflatie is voor Frankrijk 90%, voor Duitsland 80% en voor Nederland 70%. Zweden heeft met 34% de laagste gevoeligheid.

[Voor zij die nu denken dat landen met een hoge schuldratio het gemakkelijker hebben om die af te bouwen: dat klopt niet. Een hogere schuldratio betekent ook hogere interestbetalingen op die hogere schuld. Deze staan in kolom 9 van de tabel. Zoals te zien is, is het nadeel ten gevolge van de hogere interestbetalingen (soms veel) groter dan het voordeel ten gevolge van hogere inflatie.]

Specifiek voor België is dit een gevaarlijke situatie: onze lonen zijn gekoppeld aan de inflatie, waardoor de burgers zich (op korte termijn!) geen zorgen hoeven te maken over een hoge inflatie. Er zal dus weinig democratische controle zijn op de overheid om de inflatie in toom te houden. Tegelijk heeft de overheid alle belang bij een hoge inflatie om de staatsschuld beheersbaar te houden, en hoeft ze dus weinig controle te vrezen op haar inflatiebeleid.

De inflatie heeft de Belgische overheid dus beter geholpen dan onze buurlanden (behalve UK) om de staatsschuld beheersbaar te houden. Maar de inflatie is ook hoger uitgevallen dan in die buurlanden (behalve UK). Door de indexatie van de Belgische lonen, zijn deze mee gestegen met deze hogere inflatie. Ik heb geen goed zicht op de stijging van de loonkosten in onze buurlanden, maar als zij geen loonopslag gehad hebben bovenop de inflatie, dan hebben we concurrentiekracht verloren.

Dat betekent dat we deze concurrentiekracht kunnen terugwinnen door een indexsprong. Dat is niet aangenaam, maar anderzijds heeft de hogere inflatie er wel toe bijgedragen dat de Belgische overheid haar schuld beter kon beheersen. Misschien een magere troost, maar toch iets…

——————————-

Formele afleiding van de gevoeligheid van de vermindering van de schuldratio ten opzichte van inflatie.

Stel jaar 1 en 2, met een BBP1 en BBP2 en een schuld D1 en schuld D2. In jaar 2 is er een inflatie van i%.

De verandering van de schuldratio van jaar 1 naar jaar 2 is dan:

met inflatie: D2/BBP2 – D1/BBP1  (1)

zonder inflatie: D2/BBP2reëel – D1/BBP1   (2)

Om de impact van de inflatie te kennen op de vermindering van de schuldratio moeten we (1) aftrekken van (2). Dat geeft:

D2/BBP2reëel – D2/BBP2    (3)

De teller en noemer van de eerste term vermenigvuldigen met 1+i:

D2 * (1+i) / [BBP2reëel * (1+i)] – D2/BBP2   (4)

Het BBP2 is gelijk aan het reële BBP, vermeerderd met de inflatie: BBP2 = BBP2reëel * (1+i)     (5)